Hyperbolic Functions
In these lessons, we will look at Hyperbolic Functions, Hyperbolic Identities, Derivatives of Hyperbolic Functions and Derivatives of Inverse Hyperbolic Functions and how to evaluate them. We will look at the graphs of some Hyperbolic Functions and the proofs of some of the Hyperbolic Identities.
Related Pages
Hyperbolic Functions
Integrating Hyperbolic Functions
Calculus: Derivatives
Calculus Lessons
The following tables give the Definition of the Hyperbolic Function, Hyperbolic Identities, Derivatives of Hyperbolic Functions and Derivatives of Inverse Hyperbolic Functions. Scroll down the page for more examples and solutions.
Example:
Differentiate 
Solution:
Using the table above and the Chain Rule.
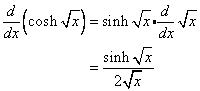
Example:
Find the derivative of 
Solution:
Using the above table and the Chain Rule
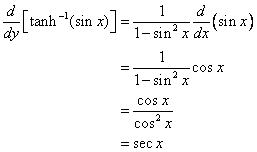
Hyperbolic Functions And Their Derivatives
Hyperbolic Functions - The Basics
This video gives the definitions of the hyperbolic functions,
a rough graph of three of the hyperbolic functions: y = sinh x, y = cosh x, y = tanh x
evaluate a few of the functions at different values: sinh(0), cosh(0), tanh(1)
and justify a couple of identities: cosh x + sinh x = ex, sinh(2x) = 2sinh x cosh x, sinh(2) = 2sinh x cosh x.
Introduction To Hyperbolic Functions
This video provides a basic overview of hyperbolic function. The lesson defines the hyperbolic functions, shows the graphs of the hyperbolic functions, and gives the properties of hyperbolic functions.
Hyperbolic functions are exponential functions that share similar properties to trigonometric functions.
Hyperbolic Functions Properties
The point (cos(t), sin(t)) is on the unit circle x2 + y2 = 1.
The point (cosh(t), sinh(t)) is on the hyperbola x2 - y2 = 1.
Graphs of hyperbolic functions: f(x) = sinh(x), f(x) = csch(x), f(x) = cosh(x), f(x) = sech(x), f(x) = tanh(x), f(x) = coth(x).
Hyperbolic Functions In Real Life: Catenary
The catenary is the curve formed by a hanging cable or chain under its own weight when
supported only at its ends.
Hyperbolic Functions - Derivatives
This video shows the formulas for the derivatives of the hyperbolic functions and finds a few derivatives.
Examples: Find the derivative
f(x) = tanh(4x)
f(x) = sinh x tanh x
Inverse Hyperbolic Functions - Derivatives
This video gives the formulas for the derivatives on the inverse hyperbolic functions and does 3 examples of finding derivatives.
Example: Find the derivatives:
y = x2sinh-1(2x)
\(y = {\tanh ^{ - 1}}\sqrt x \)
\(y = \sec {h^{ - 1}}\sqrt {1 - x} \)
Proof Of Hyperbolic Identities
This video shows a proof of one of the properties of hyperbolic functions.
Prove a Property of Hyperbolic Functions: cosh2x - sinh2x = 1
Prove a Property of Hyperbolic Functions: (tanh(x))2 + (sech(x))2 = 1
Prove a Property of Hyperbolic Functions: sinh(x+y) = sinh(x)cosh(y)+cosh(x)sinh(y)
Prove a Property of Hyperbolic Functions: (sinh(x))2 = (-1+cosh(2x))/2
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.