Decimals - Grade 5

Related Pages
Decimal Place Value
Decimal Worksheets
More Lessons for Grade 5 Math

Model Decimals

1. Using decimals extends the place value system to represent parts of a whole.
   The use of a decimal point is a symbol that separates the tenths from the ones, or the ‘part from the whole’. For example, in the number 4.2, the decimal point separates the 4 ones and the 2 tenths.

2. The base ten place value system is built on symmetry around the ones place and the decimal.

3. Decimals can represent parts of a whole, as well as mixed numbers.

4. Decimals can be interpreted and read in more than one way. For example, 4.3 may be renamed 43 tenths.

5. Decimals can be renamed as other decimals or fractions. For example, 800/1000 or 0.800 can be renamed as 80/100 or 0.80. It can also be renamed as 8/10 or 0.8
   Take note that
   0.5 or 0.50 or 0.500 are all equal to 1/2
   0.25 or 0.250 are both equal 1/4
   0.75 and 0.750 are equal to 3/4

We can use a thousands grid to model decimals.

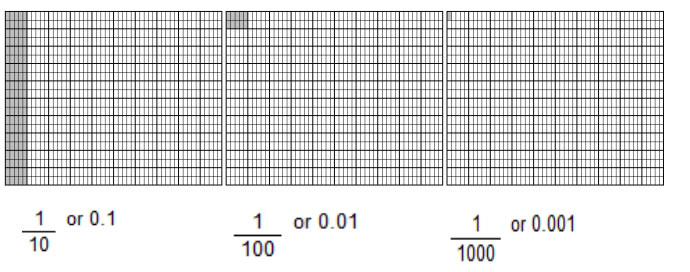
The following shaded grid can be used to represent the number 3.146

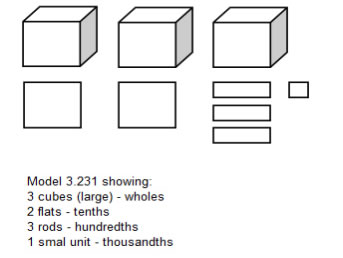
We can also use base ten blocks to model decimals.
The following can be used to represent the number 3.231

Meter sticks can also be used to represent decimals. Measuring to the nearest millimeter is one thousandths of a meter. Centimeters are hundredths of a meter and decimeters are tenths of a meter.

Model Decimals
Model decimals on grids and on number lines.

• Show Video Lesson

Decimals in Expanded Form

For Example:
45.23 = 40 + 5 + 0.2 + 0.03
or
45.23 = (4 × 10) + (5 × 1) + (2 × 0.1) + (3 × 0.01).

50.302 = 50 + 0.3 + 0.002
or
50.302 = (5 × 10) + (3 × 0.1) + (2 × 0.001).

Decimals - Expanded Form
Reading/writing decimals in numeric, word, and expanded form.

Example:

1. Write in expanded form:
   a. 9.45
   b. 0.21
   c. 8.878
   d. 0.3911

• Show Video Lesson

Compare Decimals

We can compare decimals using place value. For example:
0.02 < 0.2 because 0 tenths is less than 2 tenths
0.021 > 0.01 because 2 hundredths is greater that 1 hundredths

We can compare decimals using a benchmark number. For example:
0.021 < 0.2 because 0.021 is less than 0.1 and 0.2 is greater than 0.1
0.8 > 0.423 because 0.8 is more than half and 0.423 is less than half.

We can compare using equivalent decimals with same number of digits. For example:
0.34 > 0.3 because 0.34 > 0.30 (34 hundredths > 30 hundredths)
8.302 < 8.32 because 8.302 < 8.320 (302 thousandths < 320 thousandths)

Ordering & Comparing Decimals

• Show Video Lesson

Estimate and Round Decimals

We can round decimals to simpler decimals.

For Example: 2.9286
can be rounded to 2.929 (nearest thousandths)
can be rounded to 2.93 (nearest hundredths)
can be rounded to 2.9 (nearest tenths)
can be rounded to 3 (nearest ones)

Estimating and Rounding with Decimals

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.