Coterminal Angles

Related Pages
Reference Angles
More Lessons on Trigonometry
Angles
More Geometry Lessons

An angle is said to be in standard position if it is drawn on the Cartesian plane (x-y plane) on the positive x-axis and turning counter-clockwise (anti-clockwise).

The initial side of an angle is the ray where the measurement of an angle starts.

The terminal side of an angle is the ray where the measurement of an angle ends.

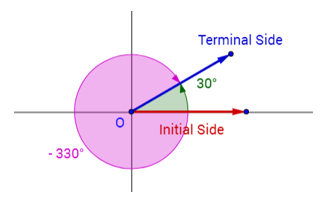
Co-terminal angles are angles which when drawn at standard position share a terminal side. For example, 30°, -330°, 390° are all coterminal.

The following diagram shows the coterminal angles 30°, -330°. Scroll down the page for more examples and solutions.

We can find the coterminal angles of a given angle by using the following formula:
Coterminal angles of a given angle θ may be obtained by either adding or subtracting a multiple of 360° or 2π radians. 

Coterminal of θ = θ + 360° × k  if θ is given in degrees.

Coterminal of θ = θ + 2π × k if θ is given in radians.

Two angles are coterminal if the difference between them is a multiple of 360° or 2π.

Example:
Determine if the following pairs of angles are coterminal
a) 10°, 370°
b) –520°, 200°
c) –600°, –60°

Solution:
a) 10° – 370° = –360° = –1(360°), which is a multiple of 360°
So, 10° and 370° are coterminal.

b) –520° – 200° = –720° = –2(360°), which is a multiple of 360°
So, –520 and 200° are coterminal.

c) –600° – (–60°) = –540°, which is not a multiple of 360°
So, –600° and –60° are not coterminal.

How to find Coterminal Angles?
This video discusses what it means for two angles to be coterminal, and discuss a quick method on how to decide if two angles are in fact coterminal. It also shows a couple of examples of finding angles that are coterminal to each other.

Examples:
a) Which of the following angles is coterminal with an angle of 135°?
185°, 495°, -30°

b) Which of the following angles is coterminal with an angle of 135°?
105°, 45°, 90°

• Show Video Lesson

How to decide if angles are coterminal or not?

Examples:
a) Which of these is NOT a pair of coterminal angles?
i) -400°, -40°
ii) 340°, -50°

b) Which of these is NOT a pair of coterminal angles?
i) 4°, 724°
ii) -15°, -385°

• Show Video Lesson

Basic Cartesian Coordinate System, Angles in Standard Position, Coterminal Angles
Coterminal angles are two different angles (rotations) with the same terminal side.

Examples:

1. What is the first positive angle coterminal with 96°?
2. What is the first negative angle coterminal with 96°?
3. What quadrant does the terminal side lie in for an angle of 920°?
4. What quadrant does the terminal side lie in for an angle of -1100°?

• Show Video Lesson

Coterminal Angles, Complementary Angles, Supplementary Angles in Radians

Examples:

1. What is the first positive angle coterminal with π/6?
   
2. What is the first negative angle coterminal with π/6?
   
3. Are the following angles coterminal: π/3 and 19π/3
   

• Show Video Lesson

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.