Conic Sections - Hyperbolas
A series of free, online video lessons with examples and solutions to help Algebra students learn about about hyperbola conic sections.
Related Pages
Conic Sections: Hyperbolas 2
Conic Sections: Circles
Conic Sections: Ellipses
Conic Sections: Parabolas
The following diagrams show the conic sections: circle, ellipse, parabola, hyperbola. Scroll down the page for examples and solutions on Hyperbolas.
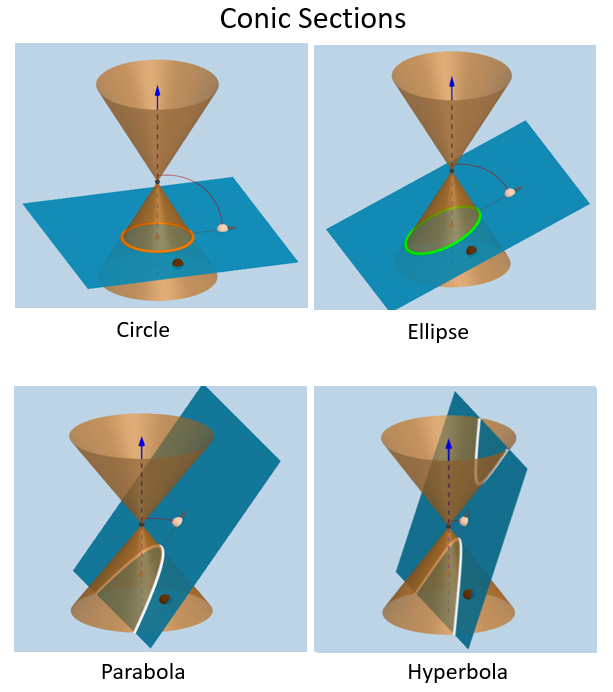
A hyperbola is a type of conic section that is formed by intersecting a cone with a plane, resulting in two parabolic shaped pieces that open either up and down or right and left. Similar to a parabola, the hyperbola pieces have vertices and are asymptotic. The hyperbola is the least common of the conic sections.
How To Talk About Hyperbolas
Graphing A Hyperbola Given In Standard Form
This video defines a hyperbola and explains how to graph a hyperbola given in standard form.
Graphing A Hyperbola Given In General Form
This video explains how to graph a hyperbola in general form.
Conic Sections: Introduction To Hyperbolas
Continuation Of The Intro To Hyperbolas
This lesson covers covers writing the equation of parabolas given certain information like the focus and vertex or vertex and directrix.
Part 3 Of The Intro To Hyperbolas
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.