Complementary Angles And Supplementary Angles
Related Pages
Pairs Of Angles
Types Of Angles
More Geometry Lessons
In these lessons, we will learn
- about complementary angles Click here
- about supplementary angles Click here
- how to solve problems involving complementary and supplementary angles Click here
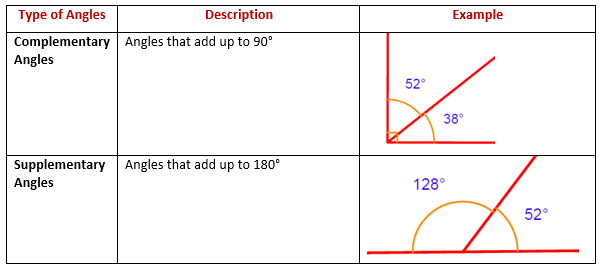
The following table gives a summary of complementary and supplementary angles. Scroll down the page if you need more explanations about complementary and supplementary angles, videos and worksheets.
Printable & Online Geometry Worksheets
What Are Complementary Angles
Two angles are called complementary angles if the sum of their degree measurements equals 90 degrees (right angle). One of the complementary angles is said to be the complement of the other.
The two angles do not need to be together or adjacent. They just need to add up to 90 degrees. If the two complementary angles are adjacent then they will form a right angle.
 |
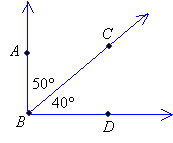∠ABC is the complement of ∠CBD |
 |
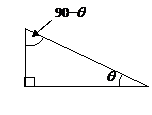In a right triangle, the two acute angles are complementary. This is because the sum of angles in a triangle is 180˚ and the right angle is 90˚. Therefore, the other two angles must add up to 90˚. |
Example:
x and y are complementary angles. Given x = 35˚, find the value y.
Solution:
x + y = 90˚
35˚ + y = 90˚
y = 90˚ – 35˚ = 55˚
Worksheets for Complementary Angles
What Are Supplementary Angles
Two angles are called supplementary angles if the sum of their degree measurements equals 180 degrees (straight line) . One of the supplementary angles is said to be the supplement of the other.
The two angles do not need to be together or adjacent. They just need to add up to 180 degrees. If the two supplementary angles are adjacent then they will form a straight line.
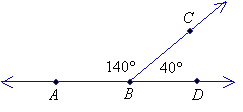
∠ABC is the supplement of ∠CBD
Example:
x and y are supplementary angles. Given x = 72˚, find the value y.
Solution:
x + y = 180˚
72˚ + y = 180˚
y = 180˚ –72˚ = 108˚
Worksheets for Supplementary Angles
A mnemonic to help you remember:
The C in Complementary stands for Corner, 90˚
The S in Supplementary stands for Straight, 180˚
Video Lessons
Have a look at the following videos for further explanations of complementary angles and supplementary angles:
How To Identify And Differentiate Complementary And Supplementary Angles?
This video describes complementary and supplementary angles with a few example problems. It will also explain a neat trick to remember the difference between complementary and supplementary angles.
Examples:
- Find x if these angles are complementary angles.
- Find n and the missing angle if these angles are complementary angles.
- Find x if these angles are supplementary angles.
- Find y and the missing angles if these angles are supplementary angles.
How To Find The Measure Of Complementary Angles Using Algebra?
Step 1: Make sure that the angles are complementary.
Step 2: Setup a solvable equation.
Step 3: Solve the equation.
Example:
∠1 = 8x + 6<br
∠2 = 19x + 3
∠1 and ∠2 are complementary.
Solve for x.
Complementary And Supplementary Angles Word Problem
Complementary Word Problem
How to solve a word problem about its angle and its complement?
Example:
The measure of an angle is 43° more than its complement. Find the measure of each angle.
Complementary And Supplementary Angles
What it means for angles to be complementary and supplementary and do a few problems to find complements and supplements for different angles.
Examples:
-
Find the measure of the complementary angle for each of the following angles:
a) 7°
b) 18°
c) 72° -
Find the measure of the supplementary angle for each of the following angles:
a) 124°
b) 75°
Complementary And Supplementary Angles Word Problems
Create a system of linear equations to find the measure of an angle knowing information about its complement and supplement.
Example:
The supplement of angle y measures 12x + 4 and the complement of the angle measures 6x. What is the
measure of the angle?
Word Problems On Complementary And Supplementary Angles
Examples:
- The measure of an angle is 14 degrees less than the measure of its complement. Find the measures of the two angles.
- The measure of an angle is 6 degrees more than twice the measure of its supplement. Find the measures of the two angles.
- The measure of the supplement of an angle is 20 degrees less than 4 times the measure of the angle. Find the measures of the two angles.
- The supplement of an angle is 12 more than 3 times the complement. Find the angle, the complement and the supplement.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.