Complement Of The Intersection Of Sets and Symmetric Difference
In these lessons, we will learn the complement of the intersection of sets, the symmetric difference of two sets and the symmetric difference of three sets.
Related Pages
Intersection Of Two Sets
Intersection Of Three Sets
Venn Diagrams
More Lessons On Sets
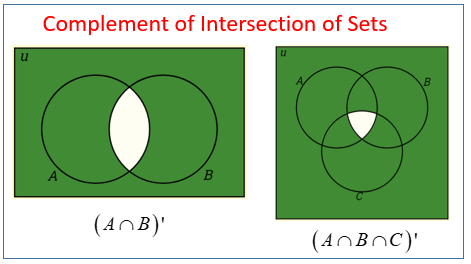
The complement of the set X ∩ Y is the set of elements that are members of the universal set U but not members of X ∩ Y. It is denoted by (X ∩ Y) ’.
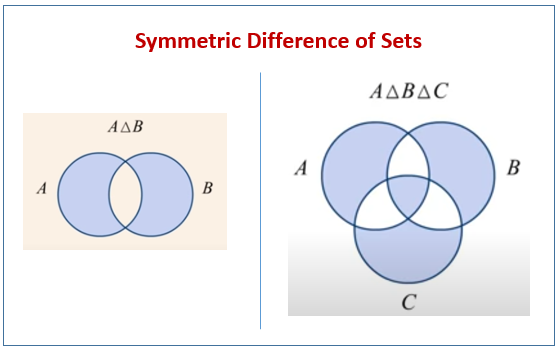
The symmetric difference of two sets is the collection of elements which are members of either set but not both - in other words, the union of the sets excluding their intersection. Forming the symmetric difference of two sets is simple, but forming the symmetric difference of three sets is a bit trickier.
The following Venn Diagrams show the Complement of the Intersection of Two Sets and the Complement of the Intersection of Three Sets. Scroll down the page for examples and solutions.
The following Venn Diagrams show the Symmetric Difference of Two Sets and the Symmetric Difference of Three Sets. Scroll down the page for examples and solutions.
Example:
Suppose U = set of positive integers less than 10,
X = {1, 2, 5, 6, 7} and Y = {1, 3, 4, 5, 6, 8} .
a) Draw a Venn diagram to illustrate ( X ∩ Y ) ’
b) Find ( X ∩ Y ) ’
Solution:
a) First, fill in the elements for X ∩ Y = {1, 5, 6}
Fill in the other elements for X and Y and for U
Shade the region outside X ∩ Y to indicate (X ∩ Y ) ’
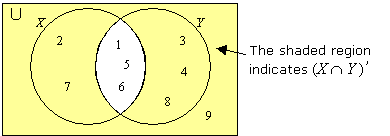
b) We can see from the Venn diagram that
(X ∩ Y ) ’ = {2, 3, 4, 7, 8, 9}
Or we find that X ∩ Y = {1, 5, 6} and so
(X ∩ Y ) ’ = {2, 3, 4, 7, 8, 9}
Symmetric Difference of two sets and three sets
Symmetric Difference of Sets
Definition and properties of the symmetric difference of two sets.
Learn the difference of sets
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.