Addition Law, Multiplication Law and Bayes Theorem
In these lessons we will look at some laws or formulas of probability: the Addition Law, the Multiplication Law and the Bayes’ Theorem or Bayes’ Rule.
Related Pages
Probability Tree Diagrams
Probability Without Replacement
Theoretical vs. Experimental Probability
More Lessons On Probability
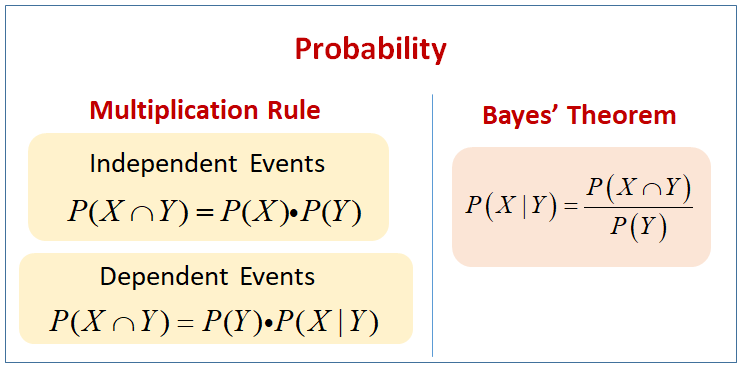
The following diagram shows the Addition Rules for Probability: Mutually Exclusive Events and Non-Mutually Exclusive Events. Scroll down the page for more examples and solutions on using the Addition Rules.
Addition Law of Probability
The general law of addition is used to find the probability of the union of two events. The expression 
denotes the probability of X occurring or Y occurring or both X and Y occurring.
The Addition Law of Probability is given by
where X and Y are events.
If the two events are mutually exclusive, the probability of the union of the two events is the probability of the first event plus the probability of the second event. Since mutually exclusive events do not intersect, nothing has to be subtracted.
If X and Y are mutually exclusive, then the addition law of probability is given by
Multiplication Law of Probability
The following diagram shows the Multiplication Rules for Probability (Independent and Dependent Events) and Bayes' Theorem. Scroll down the page for more examples and solutions on using the Multiplication Rules and Bayes' Theorem.
The probability of the intersection of two events 
is called joint probability.
The Multiplication Law of Probability is given by
The notation is the intersection of two events and it means that both X and Y must happen. 
denotes the probability of X occurring given that Y has occurred.
When two events X and Y are independent, 
If X and Y are independent then the multiplication law of probability is given by
Bayes’ Theorem or Bayes’ Rule
The Bayes’ Theorem was developed and named for Thomas Bayes (1702 – 1761). Bayes’ rule enables the statistician to make new and different applications using conditional probabilities. In particular, statisticians use Bayes’ rule to ‘revise’ probabilities in light of new information.
The Bayes’ theorem is given by
Bayes’ theorem can be derived from the multiplication law
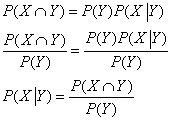
Bayes’ Theorem can also be written in different forms
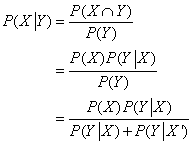
Bayes' Theorem Formulas
The following video gives an intuitive idea of the Bayes' Theorem formulas: we adjust our perspective (the probability set) given new, relevant information.
Formally, Bayes' Theorem helps us move from an unconditional probability to a conditional probability.
Conditional Probability and Bayes' Theorem
Example:
A certain virus infects one in every 400 people. A test used to detect the virus in a person is positive 85% of the time if the person has the virus and 5% of the time if the person does not have the virus. (This 5% result is called a false positive). Let A be the event “the person has the virus” and B be the event “the person tests positive”.
a) Find the probability that a person has the virus given that they have tested positive, i.e. find P(A|B). Round your answer to the nearest hundredth of a percent.
b) Find the probability that a person does not have the virus given that they test negative, i.e. find P(A'|B'). Round your answer to the nearest hundredth of a percent.
Bayes' Theorem Word Problem
The following video illustrates the Bayes' Theorem by solving a typical problem.
Example:
1% of the population has X disease. A screening test accurately detects the disease for 90% if people with it. The test also indicates the disease for 15% of the people without it (the false positives). Suppose a person screened for the disease tests positive. What is the probability they have it?
Errata: P(D|T)= .009/.1575 = .0571
Bayes' formula is evaluated using a table to organize data. (Same problem as above)
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.