Trigonometric Ratios

The basic trigonometric ratios (often called “trig ratios”) define relationships between the angles and side lengths of a right-angled triangle.

There are three primary trigonometric ratios:

1. Sine (sin)
2. Cosine (cos)
3. Tangent (tan)

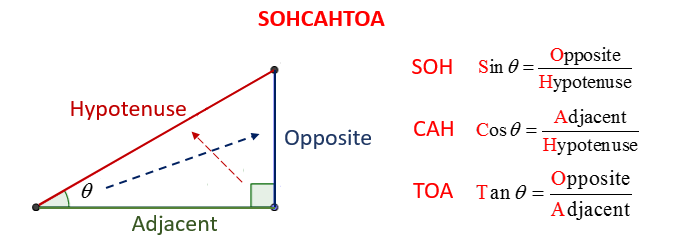
The following diagram shows the trigonometric ratios using SOHCAHTOA. Scroll down the page if you need more examples and solutions on how to use the trigonometric ratios.

 

Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets

Sides of a Right-Angled Triangle (relative to an angle θ (theta)
Consider a right-angled triangle with one of its acute angles labeled as θ (theta):

1. Hypotenuse (Hyp): The longest side of the triangle, always opposite the right angle.
2. Opposite (Opp): The side directly across from the angle θ.
3. Adjacent (Adj): The side next to the angle θ, that is not the hypotenuse.

The Three Primary Trig Ratios (SOH CAH TOA)
This mnemonic is incredibly helpful for remembering these:
1. Sine (sin):
SOH
The ratio of the length of the Opposite side to the length of the Hypotenuse.
\(\text{sin}\theta=\frac{\text{Opposite}}{\text{Hypotenuse}}\)

2. Cosine (cos):
CAH
The ratio of the length of the Adjacent side to the length of the Hypotenuse.
\(\text{cos}\theta=\frac{\text{Adjacent}}{\text{Hypotenuse}}\)

3. Tangent (tan):
TOA
The ratio of the length of the Opposite side to the length of the Adjacent side.
\(\text{tan}\theta=\frac{\text{Opposite}}{\text{Adjacent}}\)

How They Are Used:
These ratios allow you to:
Find unknown side lengths of a right-angled triangle if you know one side length and one acute angle.
Find unknown acute angles of a right-angled triangle if you know two side lengths.

Videos

Trigonometric Ratios: Sine

Right triangles have ratios to represent the angles formed by the hypotenuse and its legs. Sine ratios, along with cosine and tangent ratios, are ratios of the lengths of two sides of the triangle. Sine ratios in particular are the ratios of the length of the side opposite the angle they represent over the hypotenuse. Sine ratios are useful in trigonometry when dealing with triangles and circles.

How to define the sine ratio and identify the sine of an angle in a right triangle?

Identify the hypotenuse of a right triangle.
sin θ = opposite/hypotenuse

• Show Video Lesson

A word problem involving the trigonometric ratio of sine to calculate the height of a pole

Example:
A 55 ft wire connects a point on the ground to the top of a pole. The cable makes an angle of 60° with the ground. Find the height of the pole to the nearest foot.

• Show Video Lesson

Trigonometric Ratios: Cosine

Right triangles have ratios that are used to represent their base angles. Cosine ratios, along with sine and tangent ratios, are ratios of two different sides of a right triangle. Cosine ratios are specifically the ratio of the side adjacent to the represented base angle over the hypotenuse. In order to find the measure of the angle, we must understand inverse trigonometric functions.

How to use the Cosine formula (the CAH Formula) to find missing sides or angles?

Cosine θ = adjacent/hypotenuse

Example:
Find the missing side or angle
a) cos 30° = x/2
b) cos 37° = 4.2/x
c) cos θ = 63/80

• Show Video Lesson

How to apply the Sine and Cosine Ratios?

Sine, cosine are trigonometric ratios for the acute angles and involve the length of a leg and the hypotenuse of a right triangle.

Angle of elevation - When looking up at an object, the angle your line of sight makes with a horizontal line is called the angle of elevation.

Angle of depression - When looking down at an object, the angle your line of sight makes with a horizontal line is called the angle of depression.

Example:

1. Find sin U and sin W. Write each answer as a fraction and as a decimal rounded to four places.
2. Find cos S and cos R. Write each answer as a fraction and as a decimal rounded to four places.
3. You walk from one corner of a basketball court to the opposite corner. write and solve a proportion using a trigonometric ratio to approximate the distance of the walk.
4. You are at the top of a roller coaster 100 feet above the ground. The angle of depression is 44°. About how far do you ride down the hill?
5. A railroad crossing arm that is 20 feet long is stuck with an angle of elevation of 35°. Find the lengths of x and y.
6. Use a special right triangle to find the sine and cosine of a 30° angle.

• Show Video Lesson

Trigonometric Ratios: Tangent

Right triangles have ratios that are used to represent their base angles. Tangent ratios, along with cosine and sine ratios, are ratios of two different sides of a right triangle. Tangent ratios are the ratio of the side opposite to the side adjacent the angle they represent. In order to find the measure of the angle itself, one must understand inverse trigonometric functions.

How to use the Tangent formula (the TOA Formula)?

Tangent θ = opposite/adjacent

Example:
Find the missing side or angle
a) tan 28° = x/40
b) tan 41° = 1.9/x
c) tan θ = 11/8

• Show Video Lesson

Applications of Trigonometric Ratios (Word Problems Involving Tangent, Sine and Cosine)

Examples:

1. Find the area of the parallelogram.
2. A 70 foot ramp rises from the first floor to the second floor of a parking garage. The ramp makes an angle with the ground. How high above the first floor is the second floor?
3. You see Mr. Wandera flying a kite in the park. The kite string is 65 meters long. What angle does the string need to form with the ground so that the kite is 30 feet off of the ground?
4. From the top of a 100-foot lookout tower, a forest ranger spotted a fire at a 25° angle of depression. How far was the fire from the base of the lookout tower?
5. An 8 foot ladder is leaning against a wall. The ladder makes a 53° angle with the wall. How high does the ladder reach?

• Show Video Lesson

Inverse Trigonometric Functions

Once we understand the trigonometric functions sine, cosine, and tangent, we are ready to learn how to use inverse trigonometric functions to find the measure of the angle the function represents. Inverse trigonometric functions, found on any standard scientific or graphing calculator, are a vital part of trigonometry and will be encountered often in Calculus.

How to use inverse trigonometric functions to find an angle with a given trigonometric value and how to use inverse trigonometric functions to solve a right triangle?

Example:
Use the calculator to find an angle θ in the interval [0, 90] that satisfies the equation.

1. sin θ = 0.7523
   
2. tan θ = 3.54
   
3. Solve the given right triangle if a = 44.3 cm and b = 55.9 cm.
   
4. Find each angle in a 3,4,5 triangle

• Show Video Lesson

How to use inverse trig to find a missing angle?

Inverse trig functions are used to find missing angles rather than missing sides.

• Show Video Lesson

Find missing Angles - Using Inverse Sine, Cosine, Tangent

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.