3-4-5 Right Triangles
Recognizing special right triangles in geometry can help you to answer some questions quicker. A special right triangle is a right triangle whose sides are in a particular ratio. You can also use the Pythagorean theorem, but if you can see that it is a special triangle it can save you some calculations.
In these lessons, we will study
- the special right triangle called the 3-4-5 triangle.
- how to solve problems involving the 3-4-5 right triangle
- some examples of the Pythagorean Triples
3-4-5 Right Triangle
A 3-4-5 triangle is right triangle whose lengths are in the ratio of 3:4:5. When you are given the lengths of two sides of a right triangle, check the ratio of the lengths to see if it fits the 3:4:5 ratio.
Side1 : Side2 : Hypotenuse = 3n : 4n : 5n
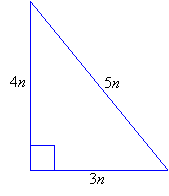
Solve problems with 3-4-5 right triangles
Example 1:
Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are 6 inches and 8 inches.
Solution:
Step 1: Test the ratio of the lengths to see if it fits the 3n : 4n : 5n ratio.
6 : 8 : ? = 3(2) : 4(2) : ?
Step 2: Yes, it is a 3-4-5 triangle for n = 2.
Step 3: Calculate the third side
5n = 5 × 2 = 10
Answer: The length of the hypotenuse is 10 inches.
Example 2:
Find the length of one side of a right triangle if the length of the hypotenuse is 15 inches and the length of the other side is 12 inches.
Solution:
Step 1: Test the ratio of the lengths to see if it fits the 3n : 4n : 5n ratio.
? : 12 : 15 = ? : 4(3) : 5(3)
Step 2: Yes, it is a 3-4-5 triangle for n = 3
Step 3: Calculate the third side
3n = 3 × 3 = 9
Answer: The length of the side is 9 inches.
Pythagorean Theorem and 3,4,5 Triangle
How to work out the unknown sides of right angles triangle?
Pythagorean Triple
3-4-5 is an example of the Pythagorean Triple. It is usually written as (3, 4, 5).
In general, a Pythagorean triple consists of three positive integers such that a2 + b2 = c2.
Other commonly used Pythagorean Triples are (5, 12, 13), (8, 15, 17) and (7, 24, 25)
Conversely, any triangle that has the Pythagorean Triples as the length of its sides would be a right triangle.
Introduction into the concepts and patterns of Pythagorean Triplets
Define and explain the Pythagorean Triples Any group of 3 integer values that satisfies the equation a2 + b2 = c2 is called a Pythagorean Triple. Therefore, any triangle that has sides that form a Pythagorean Triple must be a right triangle.
Generating Triplets
An introduction into Euclid’s formula for generating Pythagorean Triplets
The following is a list of some Pythagorean Triplets
(3,4,5), (5,12,13), (7,24,25), (8,15,17), (9,40,41), (11,60,61), (12,35,37), (13,84,85), (16,63,65), (20,21,29), (28,45,53), (33,56,65), (36,77,85), (39,80,89), (48,55,73), (65,72,97).
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.