Zeros of Polynomials
Related Topics:
Remainder Theorem
Common Core (Algebra)
Common Core for Mathematics
Suggested Learning Targets
This video explains the connection between zero, factors, and graphs of polynomial functions.
Assume we have a polynomial function of degree n
P(x) = anxn + an-1xn-1 + ... + a1x + a0
and c is a real number such that P(c) = 0.
1. The real number c is a zero or root of P(x).
2. x = c is a solution to the equation p(x) = 0.
3. (x - c) is a factor of P(x).
4. The point (c, 0) is an x-intercept of the graph of P(x).
Examples:
1. A degree 4 polynomial has zeros or roots of multiplicity 1 at x = 0 and x = 3 and a zero of multiplicity of 2 at x = -1 and has a leading coefficient of -2.
a. Give the x-intercepts of the polynomial function.
b. Write the polynomial function in factored form.
c. Graph the polynomial function.
2. Given the graph of a degree 3 polynomial.
a. Find the x-intercepts.
b. Find the real zeros or roots of the function.
c. Find the equation of the polynomial function.
Sketch the graph of polynomials using zeros, end behavior, and y intercept
Example:
Sketch the graphs of the following polynomials.
1. g(x) = x4 - 4x3 + 3x2
2. f(x) = -6x3 + 8x2 + 54x - 72
3. h(x) = -2x(x-3)3(x+5)2
End Behavior of Polynomial Functions
What is 'End Behavior'? How do I describe the end behavior of a polynomial function?
Examples:
Find the end behavior of the following polynomial function.
a) f(x) = x4 + 2x3 + 8
b) f(x) = 3x5 + 2x4 - 3x + 5 Graphing Polynomials Part 1 Graphing Polynomials Part 2
How the degree and multiplicity affect the graph of a polynomial. Finding Zeros and Factors of Polynomial Functions
Find all zeros of a polynomial function. This video covers many examples using factoring, graphing, and synthetic division.
Examples:
Find the zeros and factors of the following functions:
1. f(x) = x2 + 7x + 12
2. f(x) = x3 + x2 - 9x - 9
3. f(x) = x3 + x2 - 14x - 24
4. f(x) = x3 + 5x2 + 3x - 6
5. f(x) = x4 + x3 - 19x2 - 19x + 60
5. f(x) = x4 + 3x3 + 14x2 + 3x + 1
Remainder Theorem
Common Core (Algebra)
Common Core for Mathematics
Videos and lessons to help High School students identify zeros of polynomials when suitable factorizations are available, and use the zeros to construct a rough graph of the function defined by the polynomial.
Suggested Learning Targets
- Find the zeros of a polynomial when the polynomial is factored.
- Use the zeros of a function to sketch a graph of the function.
Common Core: HSA-APR.B.3
The following figure show how to find the zeros or roots of a polynomial function. Scroll down the page for more examples and solutions.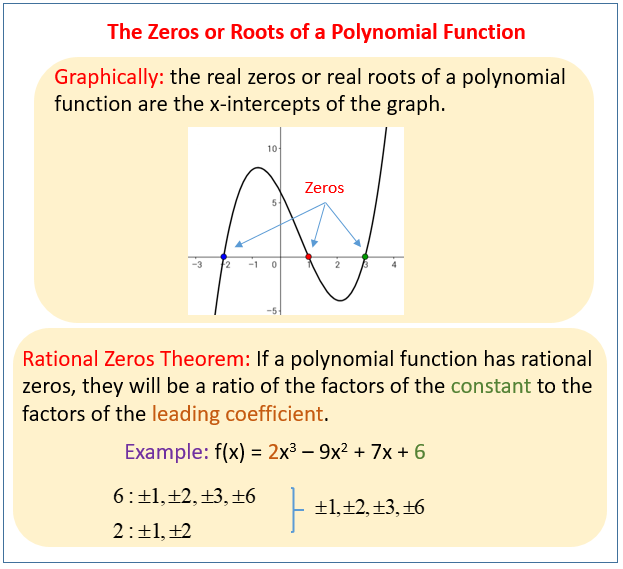
This video explains the connection between zero, factors, and graphs of polynomial functions.
Assume we have a polynomial function of degree n
P(x) = anxn + an-1xn-1 + ... + a1x + a0
and c is a real number such that P(c) = 0.
1. The real number c is a zero or root of P(x).
2. x = c is a solution to the equation p(x) = 0.
3. (x - c) is a factor of P(x).
4. The point (c, 0) is an x-intercept of the graph of P(x).
Examples:
1. A degree 4 polynomial has zeros or roots of multiplicity 1 at x = 0 and x = 3 and a zero of multiplicity of 2 at x = -1 and has a leading coefficient of -2.
a. Give the x-intercepts of the polynomial function.
b. Write the polynomial function in factored form.
c. Graph the polynomial function.
2. Given the graph of a degree 3 polynomial.
a. Find the x-intercepts.
b. Find the real zeros or roots of the function.
c. Find the equation of the polynomial function.
Example:
Sketch the graphs of the following polynomials.
1. g(x) = x4 - 4x3 + 3x2
2. f(x) = -6x3 + 8x2 + 54x - 72
3. h(x) = -2x(x-3)3(x+5)2
End Behavior of Polynomial Functions
What is 'End Behavior'? How do I describe the end behavior of a polynomial function?
Examples:
Find the end behavior of the following polynomial function.
a) f(x) = x4 + 2x3 + 8
b) f(x) = 3x5 + 2x4 - 3x + 5 Graphing Polynomials Part 1 Graphing Polynomials Part 2
How the degree and multiplicity affect the graph of a polynomial. Finding Zeros and Factors of Polynomial Functions
Find all zeros of a polynomial function. This video covers many examples using factoring, graphing, and synthetic division.
Examples:
Find the zeros and factors of the following functions:
1. f(x) = x2 + 7x + 12
2. f(x) = x3 + x2 - 9x - 9
3. f(x) = x3 + x2 - 14x - 24
4. f(x) = x3 + 5x2 + 3x - 6
5. f(x) = x4 + x3 - 19x2 - 19x + 60
5. f(x) = x4 + 3x3 + 14x2 + 3x + 1
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.