

Finding Zeros of a Polynomial Function
Related Topics:
More Lessons for PreCalculus
Math Worksheets
Videos, worksheets, solutions, and activities to help PreCalculus students learn how to find the zeros or roots of a polynomial function.
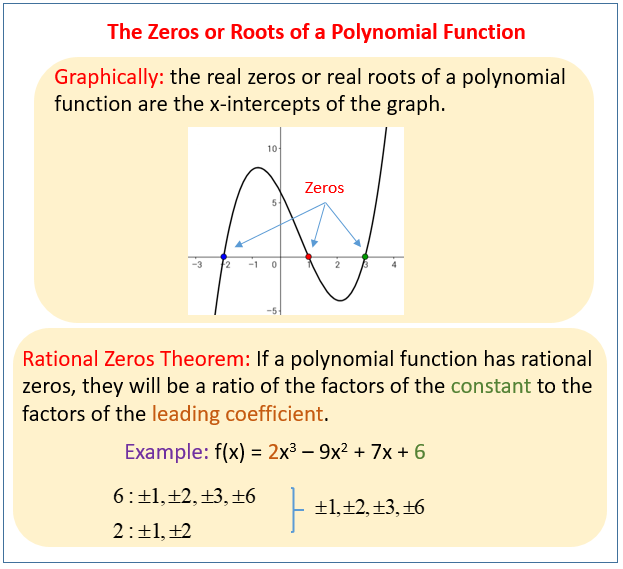
The following figure show how to find the zeros or roots of a polynomial function. Scroll down the page for more examples and solutions.
Finding the polynomial function zeros is not quite so straightforward when the polynomial is expanded and of a degree greater than two. One method is to use synthetic division, with which we can test possible polynomial function zeros found with the rational roots theorem. Once we find a zero we can partially factor the polynomial and then find the polynomial function zeros of a reduced polynomial.
How we find the zeros of a polynomial function in expanded form?
Finding all the Zeros of a Polynomial - Example 1.
This video shows how to find the remaining zeros of a polynomial given a few known zeros.
Example:
Given that one zero is x = 2 and another zero is x = 3, find the zeros and their multiplicities; let
f(x) = x4 - 10x3 + 37x2 - 60x + 36 Finding all the Zeros of a Polynomial - Example 2.
This video uses the rational roots test to find all possible rational roots; after finding one we can use long division to factor, and then repeat.
Example:
Find all the real zeros of the function:
f(x) = x3 + x2 - 10x + 8 Finding all the Zeros of a Polynomial - Example 3.
This video uses the rational roots test to find all possible rational roots; after finding one we can use long division to factor, and then repeat.
Example:
Find all the real zeros of the function:
f(x) = 3x4 - 8x3 - 37x2 + 2x + 40



More Lessons for PreCalculus
Math Worksheets
Videos, worksheets, solutions, and activities to help PreCalculus students learn how to find the zeros or roots of a polynomial function.
The following figure show how to find the zeros or roots of a polynomial function. Scroll down the page for more examples and solutions.
Finding the polynomial function zeros is not quite so straightforward when the polynomial is expanded and of a degree greater than two. One method is to use synthetic division, with which we can test possible polynomial function zeros found with the rational roots theorem. Once we find a zero we can partially factor the polynomial and then find the polynomial function zeros of a reduced polynomial.
How we find the zeros of a polynomial function in expanded form?
Finding all the Zeros of a Polynomial - Example 1.
This video shows how to find the remaining zeros of a polynomial given a few known zeros.
Example:
Given that one zero is x = 2 and another zero is x = 3, find the zeros and their multiplicities; let
f(x) = x4 - 10x3 + 37x2 - 60x + 36 Finding all the Zeros of a Polynomial - Example 2.
This video uses the rational roots test to find all possible rational roots; after finding one we can use long division to factor, and then repeat.
Example:
Find all the real zeros of the function:
f(x) = x3 + x2 - 10x + 8 Finding all the Zeros of a Polynomial - Example 3.
This video uses the rational roots test to find all possible rational roots; after finding one we can use long division to factor, and then repeat.
Example:
Find all the real zeros of the function:
f(x) = 3x4 - 8x3 - 37x2 + 2x + 40
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.