Find Zeros of a Polynomial Function
Related Topics:
More Lessons for PreCalculus
Math Worksheets
Videos, worksheets, examples, solutions, and activities to help PreCalculus students learn how to find the zeros or roots of a polynomial function.
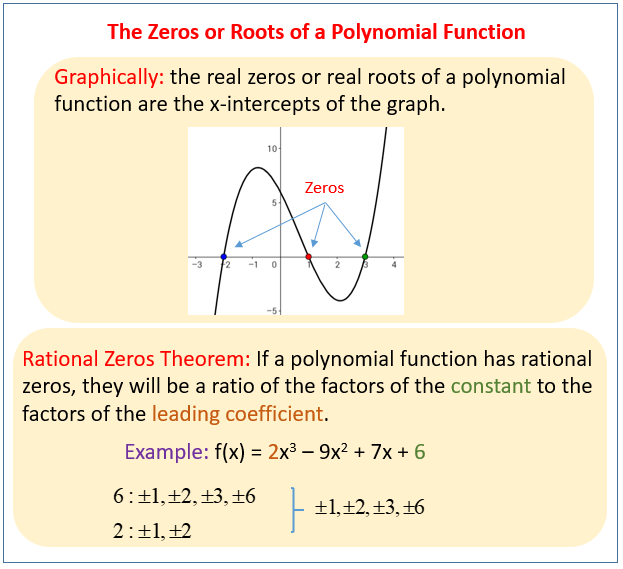
The following figure show how to find the zeros or roots of a polynomial function Graphically or using the Rational Zeros Theorem. Scroll down the page for more examples and solutions.
This video provides an introductory example of how to find the zeros of a degree 3 polynomial function.
Example:
Find all the zeros or roots of the given function graphically and using the Rational Zeros Theorem.
f(x) = x3 - 3x2 - 13x + 15 Find the Zeros of a Polynomial Function - Real Rational Zeros
This video provides an example of how to find the zeros of a degree 3 polynomial function with the help of a graph of the function.
Example:
Find all the zeros or roots of the given function.
f(x) = 6x3 - 11x2 - 26x + 15
Find the Zeros of a Polynomial Function with Irrational Zeros
This video provides an example of how to find the zeros of a degree 3 polynomial function with the help of a graph of the function. The function as 1 real rational zero and 2 irrational zeros.
Example:
Find all the zeros or roots of the given function.
f(x) = x3 - 4x2 - 11x + 2 Zeros of Polynomial Functions
How to use the graphing calculator to find real zeros of polynomial functions?
Example:
Find all the zeros or roots of the given function.
f(x) = 3x4 - 4x3 - 11x2 + 16x - 4 Finding the Zeros of a Polynomial Function
A couple of examples on finding the zeros of a polynomial function.
Example:
Find all the zeros or roots of the given functions.
f(x) = 3x3 - 19x2 + 33x - 9
f(x) = x3 - 2x2 - 11x + 52
Graphing polynomials in factored form
Graphing polynomials in factored form taking into account multiplicities of zeros.
Example:
Graph y = -3.5x2(x - 4)3(x + 3)
More Lessons for PreCalculus
Math Worksheets
Videos, worksheets, examples, solutions, and activities to help PreCalculus students learn how to find the zeros or roots of a polynomial function.
The following figure show how to find the zeros or roots of a polynomial function Graphically or using the Rational Zeros Theorem. Scroll down the page for more examples and solutions.
This video provides an introductory example of how to find the zeros of a degree 3 polynomial function.
Example:
Find all the zeros or roots of the given function graphically and using the Rational Zeros Theorem.
f(x) = x3 - 3x2 - 13x + 15 Find the Zeros of a Polynomial Function - Real Rational Zeros
This video provides an example of how to find the zeros of a degree 3 polynomial function with the help of a graph of the function.
Example:
Find all the zeros or roots of the given function.
f(x) = 6x3 - 11x2 - 26x + 15
This video provides an example of how to find the zeros of a degree 3 polynomial function with the help of a graph of the function. The function as 1 real rational zero and 2 irrational zeros.
Example:
Find all the zeros or roots of the given function.
f(x) = x3 - 4x2 - 11x + 2 Zeros of Polynomial Functions
How to use the graphing calculator to find real zeros of polynomial functions?
Example:
Find all the zeros or roots of the given function.
f(x) = 3x4 - 4x3 - 11x2 + 16x - 4 Finding the Zeros of a Polynomial Function
A couple of examples on finding the zeros of a polynomial function.
Example:
Find all the zeros or roots of the given functions.
f(x) = 3x3 - 19x2 + 33x - 9
f(x) = x3 - 2x2 - 11x + 52
Graphing polynomials in factored form
Graphing polynomials in factored form taking into account multiplicities of zeros.
Example:
Graph y = -3.5x2(x - 4)3(x + 3)
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.