Compound Interest Word Problems

Simple interest and compound interest are two different methods of calculating interest on a principal amount.

The following diagram gives a comparison of Simple Interest and Compound Interest.

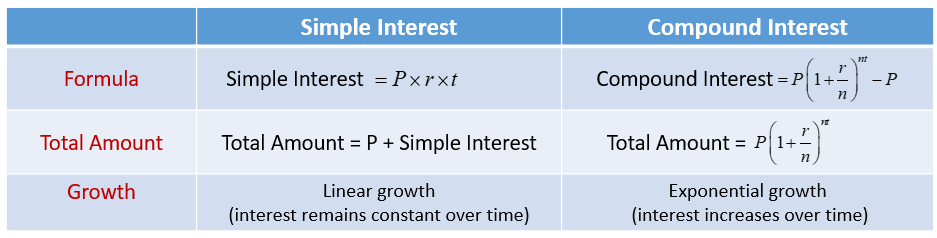
Simple Interest
Simple interest is calculated only on the principal amount over a period of time. The formula for simple interest is:
Simple Interest = P × r × t
Where:
P = principal amount, r = annual interest rate (in decimal form), t = time in years.
The total amount after interest is: Total Amount = P + Simple Interest

Compound Interest
Compound interest is calculated on the principal amount and the accumulated interest over previous periods. The interest earned or paid grows exponentially over time. The formula for compound interest is:
Compound Interest $= P{\left( {1 + \frac{{r}}{n}} \right)^{nt}} - P$
Where: P = principal amount, r = annual interest rate (in decimal form), n = number of times interest is compounded per year, t = time in years.
The total amount after interest is:
Total Amount = $= P{\left( {1 + \frac{{r}}{n}} \right)^{nt}}$

Interest Word Problems Worksheets
Interest Problems
Simple Interest Word Problems
Compound Interest Word Problems
Compound Interest & Continuously Compound Interest
Investment Word Problems

Printable & Online Algebra Worksheets

Key Differences between Simple Interest & Compound Interest

1. Growth:
   Simple interest: Linear growth.
   Compound interest: Exponential growth.
   
2. Interest Calculation:
   Simple interest: On the principal only.
   Compound interest: On the principal and accumulated interest.
   
3. Impact over Time:
   The longer the time period, the greater the difference between simple and compound interest.
   

Understanding Simple Interest and Compound Interest
Compound interest becomes significantly more beneficial over long periods. This video shows the difference between simple interest and compound interest.
Example:
Suppose you deposit $10,000 into the bank at an annual percentage rate (APR) of 6%. How much do you have 5 years later using
(a) simple interest?
(b) compound interest?

• Show Step-by-step Solutions

How to derive the Annual Compound Interest Formula?
This video shows how to derive the formula for annual compound interest
A = P(1 + APR)^Y
where A is the amount accumulated after Y years, if interest is compounded annually at the rate of APR (annual percentage rate), and P is the Principle (Initial Value)

• Show Step-by-step Solutions

Compound Interest - More than Once Per Year
If the interest is compounded more than once a year then the compound interest formula will be
$A = P{\left( {1 + \frac{{APR}}{n}} \right)^{nY}}$
where A is the amount accumulated after Y years, at the rate of APR (annual percentage rate), n is the number of times compounded per year and P is the Principle (Initial Value)
Example:
Suppose you deposit $100 at an APR of 12% compounded quarterly. How much do you have after 1 year? 2 years?

• Show Step-by-step Solutions

Compound Interest - More than Once Per Year - Part 2. This video shows another example using the compound interest formula
Example:
Suppose you would like to have $20,000 in bank 18 year from now. If you get an APR of 6%, compounded monthly, how much would you have to invest today?

• Show Step-by-step Solutions

Check out other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.