Illustrative Mathematics Grade 7, Unit 7, Lesson 12: Volume of Right Prisms
Learning Targets:
- I can explain why the volume of a prism can be found by multiplying the area of the base and the height of the prism.
Related Pages
Illustrative Math
Grade 7
Lesson 12: Volume of Right Prisms
Let’s look at volumes of prisms.
Illustrative Math Unit 7.7, Lesson 12 (printable worksheets)
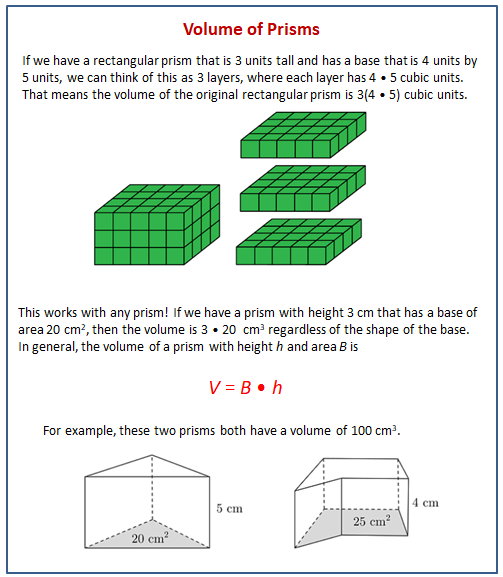
Lesson 12 Summary
The following diagrams show how a cross section is formed when we slice through a three-dimensional figure.
Lesson 12.1 Three Prisms with the Same Volume
Rectangles A, B, and C represent bases of three prisms.
- If each prism has the same height, which one will have the greatest volume, and which will have the least. Explain your reasoning.
- If each prism has the same volume, which one will have the tallest height, and which will have the shortest. Explain your reasoning.
Lesson 12.2 Finding Volume with Cubes
This applet has 64 snap cubes, all sitting in the same spot on the screen, like a hidden stack of blocks. You will always know where the stack is because it sits on a gray square. You can keep dragging blocks out of the pile by their red points until you have enough to build what you want.
Click on the red points to change from left/right movement to up/down movement.
There is also a shape on the grid. It marks the footprint of the shapes you will be building.
- Using the face of a snap cube as your area unit, what is the area of the shape? Explain or show your reasoning.
- Use snap cubes to build the shape from the paper. Add another layer of cubes on top of the shape you have built. Describe this three-dimensional object.
Open Applet - What is the volume of your object? Explain your reasoning.
- Right now, your object has a height of 2. What would the volume be a. if it had a height of 5? b. if it had a height of 8.5?
Lesson 12.3 Can You Find the Volume?
The applet has a set of three-dimensional figures. For each figure,
- Determine whether the shape is a prism.
- For each prism, additionally:
a. Find the area of the base of the prism.
b. Find the height of the prism.
c. Calculate the volume of the prism.
- Choose a figure using the slider.
- Rotate the view using the Rotate 3D Graphics tool marked by two intersecting, curved arrows.
- Note that each polyhedron has only one label per unique face. Where no measurements are shown, the faces are identical copies.
- Use the distance tool, marked with the “cm,” to click on any segment and find the height or length.
- Troubleshooting tip: the cursor must be on the 3D Graphics window for the full toolbar to appear.
Are you ready for more?
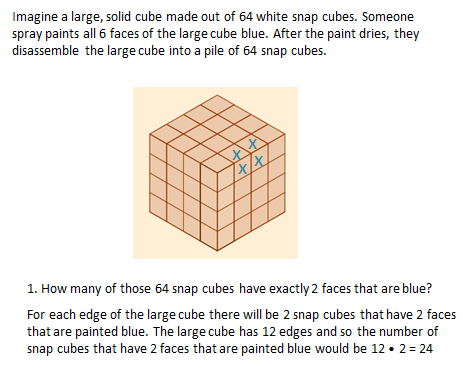
Imagine a large, solid cube made out of 64 white snap cubes. Someone spray paints all 6 faces of the large cube blue. After the paint dries, they disassemble the large cube into a pile of 64 snap cubes.
- How many of those 64 snap cubes have exactly 2 faces that are blue?
- What are the other possible numbers of blue faces the cubes can have?
-
Show Answer
0, 1 or 3 blue faces
-
Show Answer
0 blue face = 8
1 blue face = 4 · 6 = 24
3 blue faces = 8
-
Show Answer
- Try this problem again with some larger-sized cubes that use more than 64 snap cubes to build. What patterns do you notice?
-
Show Answer
if 5 · 5 · 5 = 125 snap cubes
0 blue face = 27 = 33
1 blue face = 32 · 6 = 9 · 6 = 54
2 blue faces = 3 · 12 = 36
3 blue faces = 8
-
Show Answer
Lesson 12.4 What’s the Prism’s Height?
There are 4 different prisms that all have the same volume. Here is what the base of each prism looks like.
- Order the prisms from shortest to tallest. Explain your reasoning.
- If the volume of each prism is 60 units3, what would be the height of each prism?
- For a volume other than 60 units3, what could be the height of each prism?
- Discuss your thinking with your partner. If you disagree, work to reach an agreement.
Lesson 12 Practice Problems
- a. Select all the prisms.
b. For each prism, shade one of its bases. - The volume of both of these trapezoidal prisms is 24 cubic units. Their heights are 6 and 8 units, as labeled. What is the area of a trapezoidal base of each prism?
- Two angles are complementary. One has a measure of 19 degrees. What is the measure of the other?
- Two angles are supplementary. One has a measure that is twice as large as the other. Find the two angle measures.
- Match each expression in the first list with an equivalent expression from the second list.
- Clare paid 50% more for her notebook than Priya paid for hers. Priya paid x for her notebook and Clare paid y dollars for hers. Write an equation that represents the relationship between y and x.
The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.