Vertical Angle Theorem
Related Topics:
More Lessons for Grade 9
Math Worksheets
Videos, worksheets, solutions and activities to help Geometry students learn about the vertical angle theorem.
The following figures show Vertical Angles and the Vertical Angle Theorem. Scroll down the page for more examples and solutions.
The Vertical Angle Theorem states that vertical angles are congruent.
How to prove the vertical angle theorem?
Geometry - Proving Angles Congruent - Vertical Angles Theorem (P 1)
This video introduces the components of the structure of a good proof which includes: the given information, what needs to be proved and a diagram of the information. It discusses and proves the vertical angle theorem.
All of the proofs in this lesson are of the paragraph variety.
Along with the vertical angle theorem, this two part video series discusses the congruent supplements theorem, the congruent complements theorem, and all right angles are congruent theorem.
There are a number of proofs that are completed in the same way, hopefully by the end of the second video, you will be able to complete similar proofs yourself. Geometry - Proving Angles Congruent - Vertical Angles Theorem (P 2)
Proof: Vertical angles are equal
Proving Angles are Congruent
This video introduces proof in Geometry, specifically proving that angles are congruent. The Vertical Angles Theorem, the Congruent Supplements Theorem, and the Congruent Complements Theorem are introduced.
More Lessons for Grade 9
Math Worksheets
Videos, worksheets, solutions and activities to help Geometry students learn about the vertical angle theorem.
The following figures show Vertical Angles and the Vertical Angle Theorem. Scroll down the page for more examples and solutions.
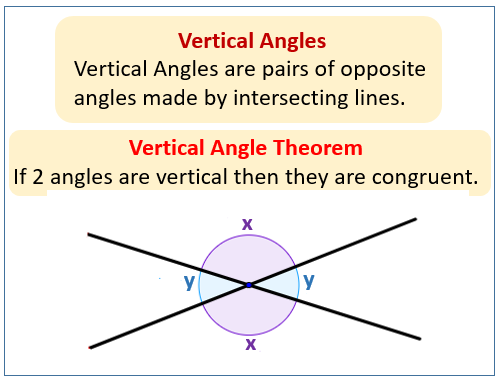
The Vertical Angle Theorem states that vertical angles are congruent.
How to prove the vertical angle theorem?
Geometry - Proving Angles Congruent - Vertical Angles Theorem (P 1)
This video introduces the components of the structure of a good proof which includes: the given information, what needs to be proved and a diagram of the information. It discusses and proves the vertical angle theorem.
All of the proofs in this lesson are of the paragraph variety.
Along with the vertical angle theorem, this two part video series discusses the congruent supplements theorem, the congruent complements theorem, and all right angles are congruent theorem.
There are a number of proofs that are completed in the same way, hopefully by the end of the second video, you will be able to complete similar proofs yourself. Geometry - Proving Angles Congruent - Vertical Angles Theorem (P 2)
This video introduces proof in Geometry, specifically proving that angles are congruent. The Vertical Angles Theorem, the Congruent Supplements Theorem, and the Congruent Complements Theorem are introduced.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.