Venn Diagram Word Problems
Related Pages
Venn Diagrams
Intersection Of Two Sets
Intersection Of Three Sets
More Lessons On Sets
More GCSE/IGCSE Maths Lessons
In these lessons, we will learn how to solve word problems using Venn Diagrams that involve two sets or three sets. Examples and step-by-step solutions are included in the video lessons.
What Are Venn Diagrams?
Venn diagrams are the principal way of showing sets in a diagrammatic form. The method consists primarily of entering the elements of a set into a circle or ovals.
Before we look at word problems, see the following diagrams to recall how to use Venn Diagrams to represent Union, Intersection and Complement.
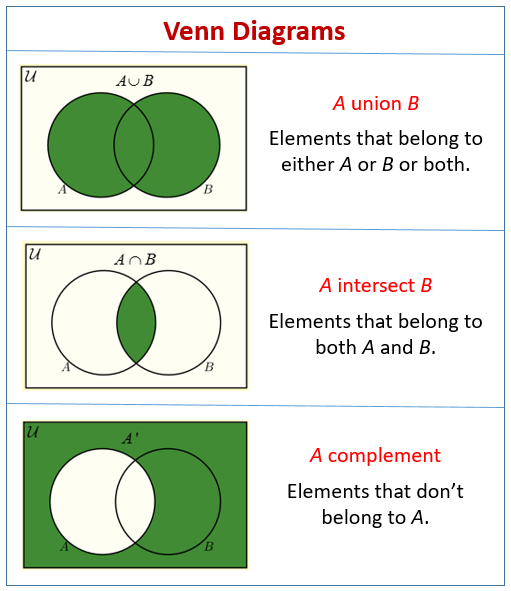
How to draw a Venn Diagram?
- Draw a rectangle to represent the universal set (U).
- Draw overlapping circles within the rectangle to represent each individual set. Clearly label each set with its name
- Fill in the Information. Start with the intersection (the overlapping region), then fill in the remaining parts of each set and the region outside all the sets.
- Use the diagram to answer the specific questions related to the sets, such as finding the number of elements in a specific region, or the number of elements in the union or intersection of two sets.
How To Solve Problems Using Venn Diagrams?
This video solves two problems using Venn Diagrams. One with two sets and one with three sets.
Problem 1:
150 college freshmen were interviewed.
85 were registered for a Math class,
70 were registered for an English class,
50 were registered for both Math and English.
a) How many signed up only for a Math Class?
b) How many signed up only for an English Class?
c) How many signed up for Math or English?
d) How many signed up neither for Math nor English?
Problem 2:
100 students were interviewed.
28 took PE, 31 took BIO, 42 took ENG, 9 took PE and BIO, 10 took PE and ENG, 6 took BIO and ENG,
4 took all three subjects.
a) How many students took none of the three subjects?
b) How many students took PE but not BIO or ENG?
c) How many students took BIO and PE but not ENG?
How And When To Use Venn Diagrams To Solve Word Problems?
Problem:
At a breakfast buffet, 93 people chose coffee and 47 people chose juice. 25 people chose both coffee
and juice. If each person chose at least one of these beverages, how many people visited the buffet?
How To Use Venn Diagrams To Help Solve Counting Word Problems?
Problem:
In a class of 30 students, 19 are studying French, 12 are studying Spanish and 7 are studying both
French and Spanish. How many students are not taking any foreign languages?
Probability, Venn Diagrams And Conditional Probability
This video shows how to construct a simple Venn diagram and then calculate a simple conditional probability.
Problem:
In a class, P(male)= 0.3, P(brown hair) = 0.5, P (male and brown hair) = 0.2
Find
(i) P(female)
(ii) P(male| brown hair)
(iii) P(female| not brown hair)
Venn Diagrams With Three Categories
Example:
A group of 62 students were surveyed, and it was found that each of the students surveyed liked at
least one of the following three fruits: apricots, bananas, and cantaloupes.
34 liked apricots.
30 liked bananas.
33 liked cantaloupes.
11 liked apricots and bananas.
15 liked bananas and cantaloupes.
17 liked apricots and cantaloupes.
19 liked exactly two of the following fruits: apricots, bananas, and cantaloupes.
a. How many students liked apricots, but not bananas or cantaloupes?
b. How many students liked cantaloupes, but not bananas or apricots?
c. How many students liked all of the following three fruits: apricots, bananas, and cantaloupes?
d. How many students liked apricots and cantaloupes, but not bananas?
Venn Diagram Word Problem
Here is an example on how to solve a Venn diagram word problem that involves three intersecting sets.
Problem:
90 students went to a school carnival. 3 had a hamburger, soft drink and ice-cream. 24 had hamburgers.
5 had a hamburger and a soft drink. 33 had soft drinks. 10 had a soft drink and ice-cream.
38 had ice-cream. 8 had a hamburger and ice-cream. How many had nothing?
(Errata in video: 90 - (14 + 2 + 3 + 5 + 21 + 7 + 23) = 90 - 75 = 15)
Venn Diagrams With Two Categories
This video introduces 2-circle Venn diagrams, and using subtraction as a counting technique.
How To Use 3-Circle Venn Diagrams As A Counting Technique?
Learn about Venn diagrams with two subsets using regions.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.