The Unit Circle Definition of Trigonometric Function

Trigonometry is about the relationships between angles and sides of triangles. While it traditionally starts with right-angled triangles (SOH CAH TOA), the unit circle provides a much more powerful and complete way to define trigonometric functions, extending them to any angle, including obtuse angles, reflex angles, and negative angles.

What is the Unit Circle?
Imagine a circle drawn on the coordinate plane with these specific features:
Its center is at the origin (0,0).
Its radius is exactly 1 unit.

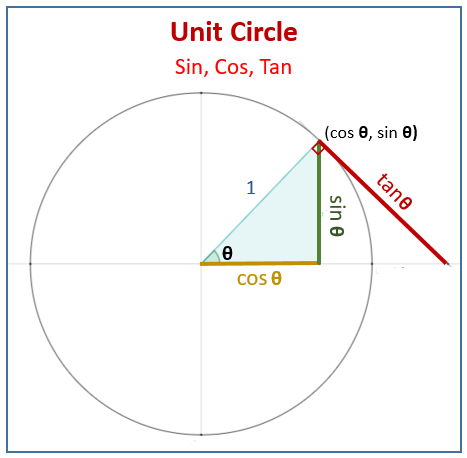
The following diagram shows the unit circle definition of the trig functions: sin, cos, and tan. Scroll down the page for more examples and solutions on the unit circle and trigonometry.

 

Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets

How the Unit Circle Defines Trigonometric Functions

1. Start with an Angle:
   Draw an angle, let’s call it θ (theta), in standard position. This means:
   The vertex of the angle is at the origin (0,0).
   The initial side of the angle always lies along the positive x-axis.
   The terminal side of the angle rotates:
   Counter-clockwise for positive angles.
   Clockwise for negative angles.
   

2. Find the Point on the Circle:
   The terminal side of your angle θ will intersect the unit circle at a unique point. Let’s call this point P(x,y).

3. Define Sine, Cosine, Tangent:
   If you draw a right triangle within the unit circle (using the point P(x,y), the origin, and the x-axis), the hypotenuse is the radius, which is 1.
   The adjacent side of this triangle has length |x|.
   The opposite side has length |y|.
   
   From SOH CAH TOA for a right triangle:
   The x-coordinate of the point P(x,y) on the unit circle is defined as the cosine of the angle θ (cosθ).
   \(\text{cos }\theta=\frac{\text{Adjacent}}{\text{Hypotenuse}}=\frac{x}{1}=x\)
   
   The y-coordinate of the point P(x,y) on the unit circle is defined as the sine of the angle θ (sinθ).
   \(\text{sin }\theta=\frac{\text{Opposite}}{\text{Hypotenuse}}=\frac{y}{1}=y\)
   
   The tangent of the angle θ (tanθ) is defined as the ratio of the y-coordinate to the x-coordinate of the point P(x,y).
   \(\text{tan }\theta=\frac{\text{sin }\theta}{\text{cos }\theta}=\frac{x}{y}=y\) for \(y \neq 0\)
   
   This shows why the x-coordinate is cosine and the y-coordinate is sine for angles in the first quadrant. The beauty of the unit circle is that this definition holds true for angles in any quadrant.
   
   Tangent as a Line Segment:
   Imagine a vertical line drawn tangent to the unit circle at the point (1,0).
   a) For any angle θ, extend the terminal side of the angle (the radius) beyond the unit circle until it intersects this vertical tangent line at x=1.
   b) The y-coordinate of this intersection point on the tangent line is the value of tan(θ).
   (In the above diagram, the tangent line shown would be congruent to this line segment. You can check for congruent triangles to proof)
   

Videos

Unit Circle Definition of Trig Functions
Using the unit circle to define the sine, cosine, and tangent functions

• Show Step-by-step Solutions

The unit circle definition of trigonometric function
Using the unit circle to extend the SOH CAH TOA definition of the basic trigonometric functions.

• Show Step-by-step Solutions

Deriving Values on the Unit Circle.
This video shows how to derive the values in the first quadrant of the unit circle.

A Trick to Remember Values on The Unit Circle
This video shows a little ’trick’ to remember the values on the unit circle in the first quadrant.

• Show Step-by-step Solutions

A way to remember the Entire Unit Circle for Trigonometry.

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.