Two Column Proofs

A two-column proof consists of a list of statements, and the reasons why those statements are true. The statements are in the left column and the reasons are in the right column. The statements consists of steps toward solving the problem.

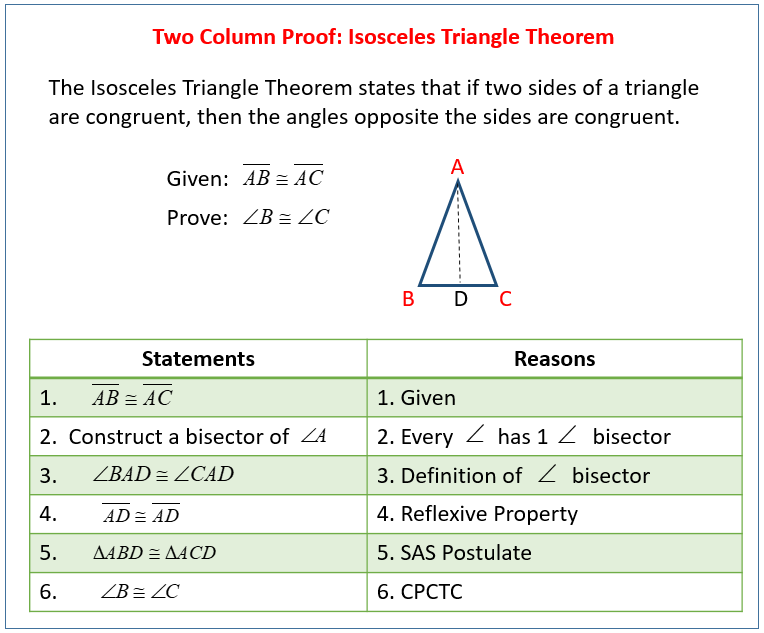
The following figure gives a Two-column Proof for the Isosceles Triangle Theorem. Scroll down the page for more examples and solutions.

 

How To Use The Two-Column Proof To Prove The Isosceles Triangle Theorem? Click here
How To Use The Two-Column Proof To Prove The Exterior Angle Theorem? Click here
How To Use Two Column Proof To Show Segments Are Perpendicular? Click here
How To Use Two Column Proof To Prove Parallel Lines? Click here
How To Use Two Column Proof To Prove a Quadrilateral is a Parallelogram? Click here

How to Write a Two-Column Proof?

1. Understand the Problem: Carefully read and understand what you are trying to prove. Identify the given information and the statement you need to reach as the conclusion.
2. Draw a Diagram (if applicable): A visual representation of the problem can often help you see the relationships between different elements. Label the diagram with the given information.
3. Start with the Given Information: The first statement(s) in your proof should be the information that is provided in the problem. The reason for these statements is “Given.”
4. Use Logical Reasoning: Apply definitions, postulates, theorems, and properties to make logical deductions from the given information and subsequent statements. Each deduction will be a new statement in your proof, and the reason will be the rule or fact that justifies that statement.
5. Work Towards the Conclusion: Continue making logical deductions until you arrive at the statement you were asked to prove. The final statement of your proof should be the conclusion.
6. Review and Verify: Once you have completed the proof, review each step to ensure that the statements are logical and the reasons are valid and accurately support the statements.

Common Reasons Used in Proofs
Given: Information provided in the problem.
Definitions: E.g., “Definition of midpoint."
Postulates: E.g., “Segment Addition Postulate."
Theorems: E.g., “Vertical Angles Theorem."
Algebraic Properties: Substitution, Addition, Subtraction, etc.

Two-Column Proof (5 steps) Practice 1

Practice writing a 2 column proof.
Example:
Given AD = 8, BC = 8, B̅C̅ ≅ C̅D̅
Prove: A̅D̅ ≅ C̅D̅

• Show Video Lesson

Two-Column Proof (7 steps) Practice 2

Practice writing two column proofs.
Example:
Given D̅E̅ ≅ F̅G̅
Prove: x = 4

• Show Video Lesson

Proof Practice (5 steps) Practice 3

Practice writing two column proofs.
Example:
Given MN = PQ
Prove: MP = NQ

• Show Video Lesson

Practice Proof 4 (Use angle addition postulate)

Practice writing 2 column proofs.
Example:
Given m∠RPS = m∠TPC, m∠TPV = m∠SPT
Prove: m∠RPV = 3(m∠RPS)

• Show Video Lesson

How To Use The Two-Column Proof To Prove The Isosceles Triangle Theorem?

The Isosceles Triangle Theorem states that if two sides of a triangle are congruent, then the angles opposite the sides are congruent.

• Show Video Lesson

How To Use The Two-Column Proof To Prove The Exterior Angle Theorem?

The Exterior Angle Theorem states that the sum of the remote interior angles is equal to the non-adjacent exterior angle.

• Show Video Lesson

How To Use Two Column Proof To Show Segments Are Perpendicular?

Use the SSS, SAS, ASA, AAS postulates.
Using triangle congruency postulates to show that two intersecting segments are perpendicular. (Diagonals of a kite)

• Show Video Lesson

How To Use Two Column Proof To Prove Parallel Lines?

Given ∠2 ≅ ∠1 ≅ ∠3
Prove: A̅B̅ || C̅D̅

• Show Video Lesson

Proving A Quadrilateral Is A Parallelogram | Geometry Proof

This video geometry lesson proves two parallelogram theorems using the two column proof.
Proof 1:
If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
Proof 2:
If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
Theorems Used: If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram and If one pair of opposite sides of a quadrilateral is both congruent and parallel, then the quadrilateral is a parallelogram to solve problems.

• Show Video Lesson

Special Parallelograms - Rhombus And Rectangle Proofs

This video uses the two column method to prove two theorems.
Proof 1:
The diagonals of a rectangle are congruent. This amounts to be a triangle proof to use CPCTC.
Proof 2:
The diagonals of a rhombus are perpendicular.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.