Trigonometric Questions with Bearings

How to solve Bearing Word Problems?

Solving bearing word problems effectively hinges on a clear understanding of bearing notation, accurate diagram construction, and the correct application of trigonometric principles like the Sine and Cosine Rules.

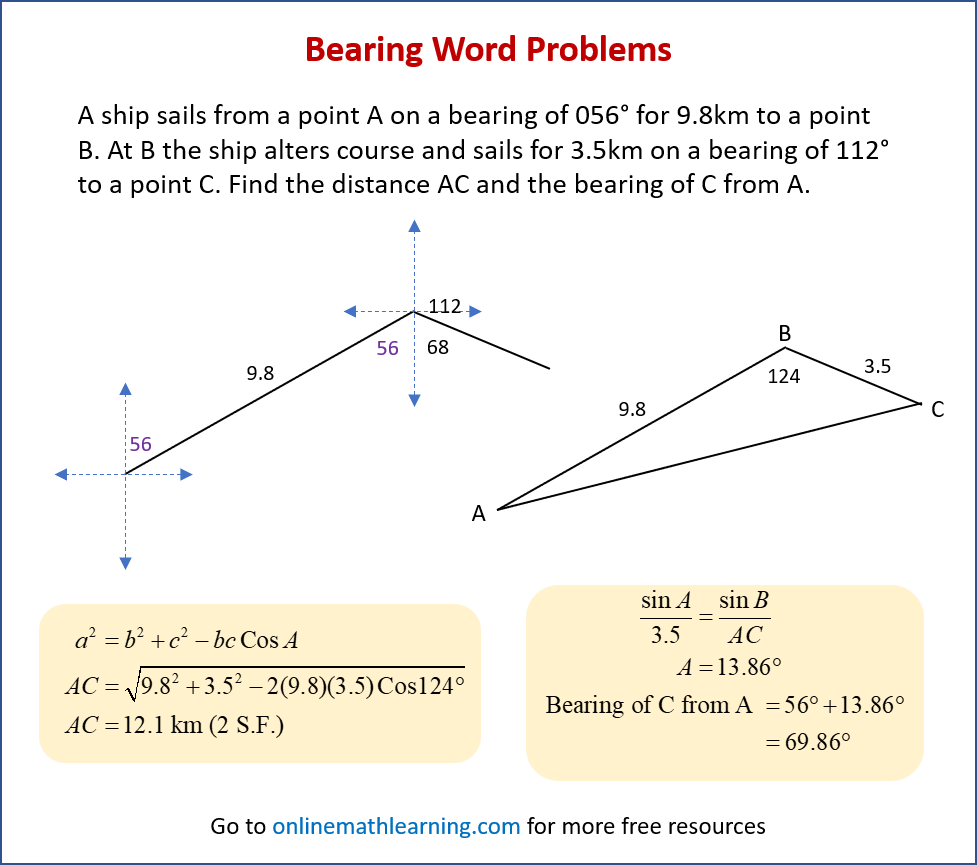
The following diagram shows how to solve a bearing word problem using the Cosine and Sine Rules. Scroll down the page for more examples and solutions.

 

Trigonometry Worksheets
Practice your skills with the following worksheets"
Printable & Online Trigonometry Worksheets

1. Understand Three-Figure Bearings:
   

• Measured clockwise from the North line.
• Always expressed with three digits, e.g., 045° (for 45°), 135°, 005°.
• The North line at any point is considered to be pointing upwards on your diagram.

2. Draw an accurate, clear, and well-labeled diagram:
   

• Begin with the initial point mentioned in the problem.
• At every point from which a bearing is measured or to which an object travels, draw a North line. These North lines must be parallel to each other.
• Carefully measure or estimate the angles clockwise from the North line for three-figure bearings.
• Label the lengths of the paths or distances between points.
• The paths and lines connecting different points will often form one or more triangles.
• Label all points, known angles, and known sides. Indicate what you need to find.

3. Determine Angles Within the Triangle:
   

• Use the properties of parallel lines and angles to find the interior angles of the triangle you’ve drawn.
• For example:
  a) The sum of angles around a point is 360°.
  b) The sum of angles on a straight line is 180°.
  c) Alternate Interior Angles (Z-angles): When a transversal line (like the path of travel) intersects two parallel North lines, alternate interior angles are equal. This is extremely useful for finding angles inside your triangle.
  d) Corresponding Angles (F-angles): Also formed by a transversal intersecting parallel lines, these angles are equal.
  e) Co-interior Angles (C-angles): These angles between parallel lines on the same side of the transversal add up to 180°.
  f) Angles in a Triangle: The sum of angles inside a triangle is 180°.
  

C2 Sine and Cosine Rule
Questions in Context Bearings
Examples:

1. Fred is standing at a point looking north. He walks on a bearing 056° for 9.8km before stopping. He then walks an additional 3.5 km on a bearing of 112° before stopping to rest. Find out how far he is away from his start point.
   
2. Sue walks around the perimeter of a triangular field. She walks west from one corner of the field for 480m before stopping at the second corner. She then walks an additional 312m on a bearing of 072° to complete the second side of the field?
   (a) How long is the third side of the field?
   (b) Find the total area of the enclosed field.
   

• Show step-by-step solutions

Sine & Cosine Rules applied to Bearings
Example:
A ship sails from a point A on a bearing of 040° for 3km to a point B. At B the ship alters course and sails for 5km on a bearing of 160° to a point C. Find the distance AC and the bearing of A from C.

• Show step-by-step solutions

Cosine Rule and Bearing Problem
Example:
Jack walks from town A for 10 miles on a bearing of 20°. Peter walks from town A for 18 miles on a bearing of 130°. How far is Jack from Peter?

• Show step-by-step solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.