Signs Of Trigonometric Ratios
In these lessons, we will examine the trigonometric ratios of angles in the four quadrants.
Related Pages
Trigonometric Graphs
Trigonometric Functions
Lessons On Trigonometry
How to remember the signs of the trigonometric functions for the four quadrants?
We can use a mnemonic like CAST or** A**ll** S**tudents **T**ake** C**alculus to remember the signs in the 4 quadrants.
The following figure shows the signs of the trigonometric functions for the four quadrants. Scroll down the page for more examples and solutions.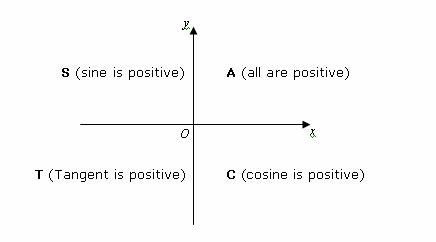 
The trigonometric ratios for 0˚, 90˚, 180˚, 270˚ and 360˚ are shown below:
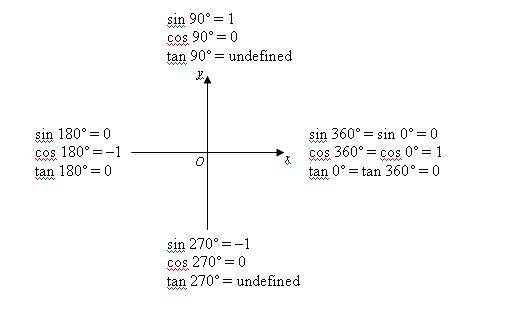
Take note of the signs of the trigonometric ratios in the following examples.
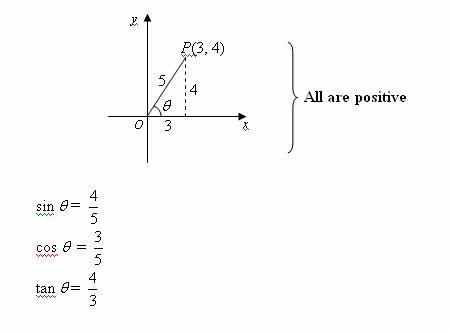
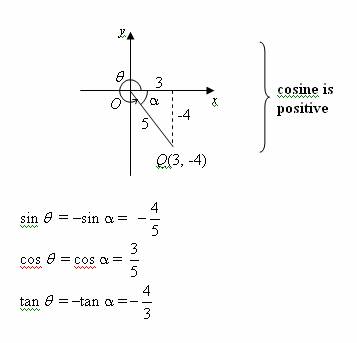
Quadrant 1 (0° < θ < 90°)
In the following diagram, θ is in the first quadrant.
Sine, cosine and tangent are all positive.
Quadrant II (90° < θ < 180°)
In the following diagram, θ is in the second quadrant.
The reference angle, α = 180° – θ
Sine is positive whereas cosine and tangent are negative.
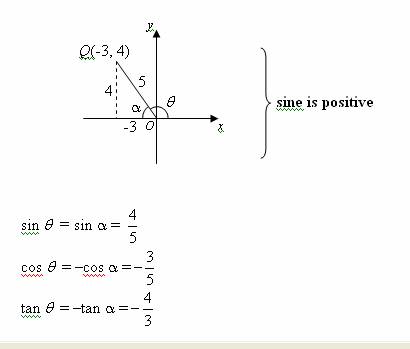
Quadrant III (180° < θ < 270°)
In the following diagram, θ is in the third quadrant.
The reference angle, α = θ – 180°
Tangent is positive whereas sine and cosine are negative.
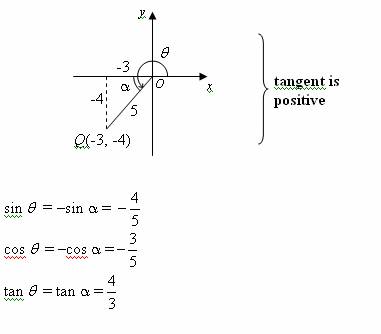
Quadrant IV (270° < θ < 360°)
In the following diagram, * θ* is in the fourth quadrant.
The reference angle, α = 360° – θ
Cosine is positive whereas sine and tangent are negative.
Example:
Determine the sign of each of the following values.
a) cos 121°
b) tan 220°
Solution:
a) cos 121° is in quadrant II (90° < 121° < 180°)
In quadrant II, only sine is positive, so cos 121° is negative.
b) tan 220° is in quadrant III (180° < 220° < 270°)
In quadrant III, tangent is positive, so tan 220° is positive.
Unit Circle, Reference Angle and Signs of Trig Functions in 4 Quadrants
Finding Trig Functions Given A Point(x, y) in Different Quadrants
Example:
Assume that θ is an angle in standard position whose terminal side contains the point (-5,12). Find the exact values of sin θ, cos θ, and tan θ.
How to Find Trig Function Values Given One Value and the Quadrant?
Example:
If tan θ = -5/12 and &theta is in quadrant IV, find all trigonometric function values for θ.
How to find all six trigonometric function values given one value (the secant) and the quadrant?
Example:
If sec θ = -2 and θ is in quadrant III, find all trigonometric function values for θ
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.