Trigonometric Ratios

Trigonometric ratios define the relationships between the angles and sides of a right-angled triangle. They are essentially ratios of the lengths of the sides of a right triangle with respect to one of its acute angles.

These ratios are constant for a given angle, regardless of the size of the right triangle. This means if you have two right triangles with the same acute angle, the ratios of their corresponding sides will be identical.

The following diagram shows the six trig ratios: Sin, Cos, Tan, Sec, Csc, and Cot. Scroll down the page for more examples and solutions on the trigonometric ratios.

 

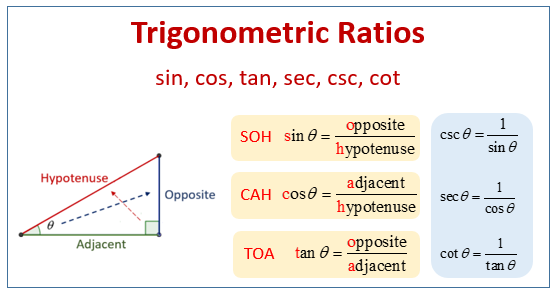
Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets

The Three Primary Trigonometric Ratios (SOH CAH TOA)
To understand these ratios, we first need to identify the sides of a right-angled triangle relative to a specific acute angle (let’s call it θ - theta).

1. Hypotenuse (H): This is always the longest side of the right triangle, and it is always opposite the 90° angle.
2. Opposite (O): This is the side directly across from the reference angle θ.
3. Adjacent (A): This is the side next to the reference angle θ that is not the hypotenuse.

A popular mnemonic to remember these three ratios is SOH CAH TOA:
SOH: \(\text{sin }\theta=\frac{\text{Opposite}}{\text{Hypotenuse}}\)
CAH: \(\text{cos }\theta=\frac{\text{Adjacent}}{\text{Hypotenuse}}\)
TOA: \(\text{tan }\theta=\frac{\text{Opposite}}{\text{Adjacent}}\)

The Three Reciprocal Trigonometric Ratios
In addition to the three primary ratios, there are three reciprocal ratios:
Cosecant (csc): The reciprocal of sine.
\(\text{csc }\theta=\frac{1}{\text{sin }\theta}\)
Secant (sec): The reciprocal of cosine.
\(\text{sec }\theta=\frac{1}{\text{cos }\theta}\)
Cotangent (cot): The reciprocal of tangent.
\(\text{cot }\theta=\frac{1}{\text{tan }\theta}\)

Six Trig Ratios: sin, cos, tan, csc, sec, and tan

Example:
Determine the six trigonometric ratios for angle A in the right triangle.

• Show Video Lesson

Trigonometry - Right Angled Triangles - Naming the Sides
In this tutorial you are shown how to name the sides of any right-angled triangle which is the first stage in solving a question in trigonometry.

• Show Video Lesson

Trigonometry - The Trig Ratios
In this tutorial you are shown how the sin, cos and tan ratios compare two sides of a right-angled triangle. You need to know this before calculating lengths and angles of right-angled triangles.

• Show Video Lesson

Trigonometric Ratios

• Show Video Lesson

How to Use Trigonometric Ratios
Trigonometric ratios are incredibly useful for:

1. Finding unknown side lengths of a right triangle when you know one side length and one acute angle.
2. Finding unknown angle measures of a right triangle when you know the lengths of two sides.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.