

Trigonometric Integrals
More Lessons for trigonometric identities
Math Worksheets
In this lesson, we will look into some techniques of integrating powers of sine, cosine, tangent and secant. We will use trigonometric identities to integrate certain combinations of trigonometric functions.
Odd Power of Sine or Cosine
To integrate an odd power of sine or cosine, we separate a single factor and convert the remaining even power.
If the power of cosine is odd (n = 2k + 1), save one cosine factor and use the identity sin2 x + cos2 x = 1 to express the remaining factors in terms of sine:
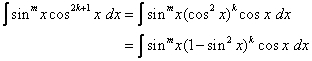
Let u = sin x then du = cos x dx
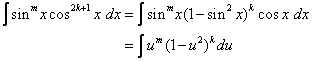
If the power of sine is odd (n = 2k + 1), save one sine factor and use the identity sin2 x + cos2 x = 1 to express the remaining factors in terms of cosine:
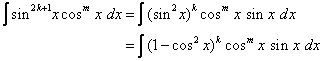
Let u = cos x then du = – sin x dx

Note: If the powers of both sine and cosine are odd, either of the above methods can be used.
Example:
Evaluate ![]()
Solution:
Step 1:
Separate one cosine factor and convert the remaining cos2 x factor to an expression involving sine using the identity sin2 x + cos2 x = 1
![]()
Step 2:
Let u = sin x then du = cos x dx

Example:
Evaluate ![]()
Solution:
Step 1:
Separate one sine factor and convert the remaining sin 4 x factor to an expression involving cos using the identity sin2 x + cos2 x = 1
![]()
Step 2:
Let u = cos x then du = – sin x dx

Even Powers of Sine and Cosine
If the powers of both the sine and cosine are even, use the half-angle identities

Example:
Find ![]()
Solution:
If we write sin2 x as 1 – cos2 x, the integral is no simpler to evaluate.
Instead, we use the half-angle formula for ![]()
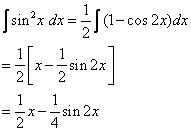
Example:
Find ![]()
Solution:
We write sin4 x as (sin2 x)2 and use a half-angle formula:
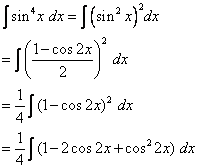
In order to evaluate cos2 2x, we use the half angle formula ![]()

Trigonometric Integrals - Part 1 of 6
The 'cookie cutter' case of products of odds powers of sine and/or odd powers of cosine is discussed.
The 'cookie cutter' case of products of even powers of sine and even powers of cosine is discussed Trigonometric Integrals - Part 3 of 6
The 'cookie cutter' case of products of even powers of secant and powers of tangent is discussed Trigonometric Integrals - Part 4 of 6
The 'cookie cutter' case of products of odd powers of tangent and powers of secant is discussed. Trigonometric Integrals - Part 5 of 6
The 'cookie cutter' case of products of sin(mx) and cos(nx) are shown Trigonometric Integrals - Part 6 of 6
3 trigonometric integrals that do not fit any one technique are discussed.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.