Properties of the Angles Of A Triangle

In these lessons, we will give a summary of the properties of the angles of a triangle.

• Triangle Sum Theorem - The sum of the 3 angles in a triangle is always 180°
• The sum of an interior angle and its adjacent exterior angle is 180°
• Exterior Angle Theorem - An exterior angle of a triangle is equal to the sum of the two opposite interior angles
• An equilateral triangle has 3 equal angles that are 60° each. An isosceles triangle has 2 equal angles, which are the angles opposite the 2 equal sides

The following figures show some Angles in Triangle Theorems: Triangle Sum Theorem, Exterior Angle Theorem. Scroll down the page for more examples and solutions.

Geometry Worksheets
Practice your Geometry skills with the following worksheets:
Printable & Online Geometry Worksheets

The angles of a triangle have the following properties:

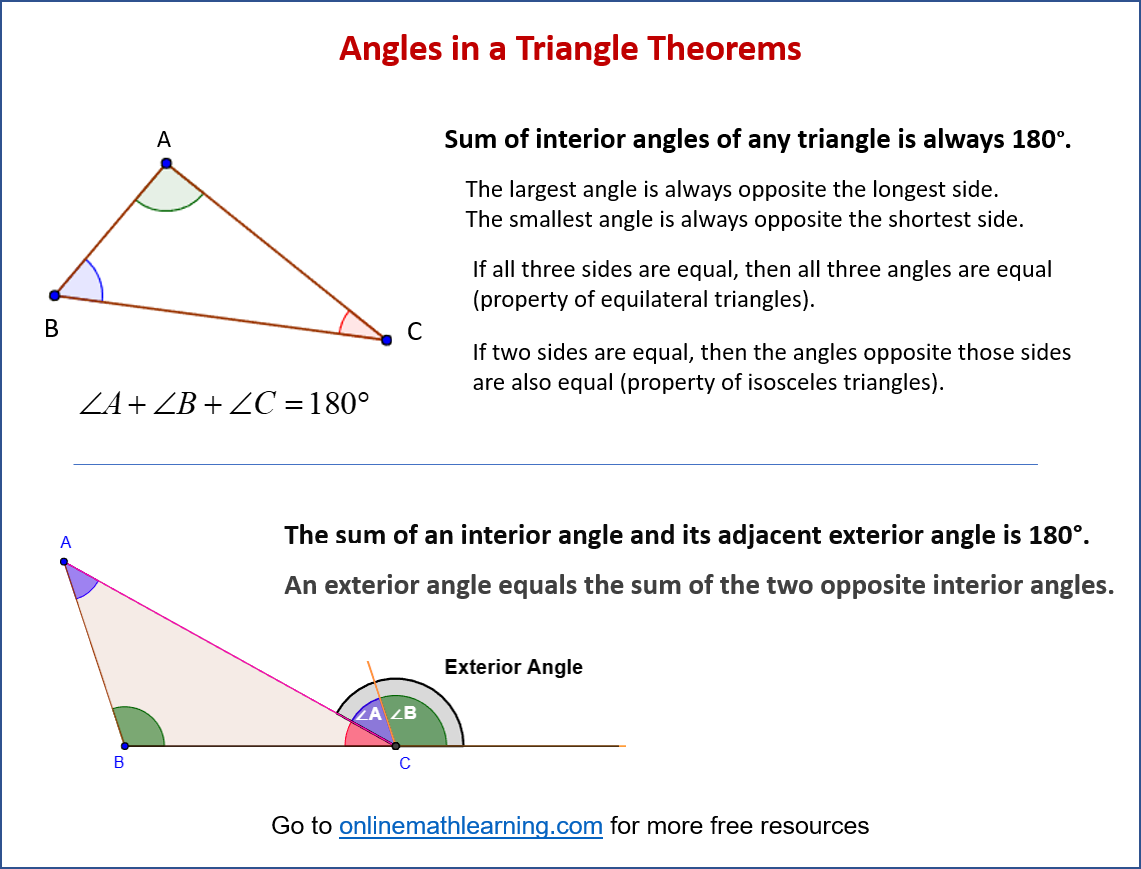
Property 1: Triangle Sum Theorem

The sum of the 3 angles in a triangle is always 180°.

Example:

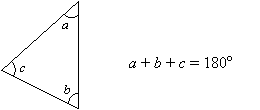
**How to prove the Triangle Sum Theorem?**
The following video shows how to prove that the sum of the angles of a triangle is 180 degrees. (Triangle Sum Theorem)

• Show Step-by-step Solutions

How to Find the Missing Angle in a Triangle Using the Triangle Sum Theorem?
Step 1: Write out the equation by adding all the angles and making them equal to 180°.
Step 2: Solve for x.
Step 3: Substitute to find the missing angles.

• Show Step-by-step Solutions

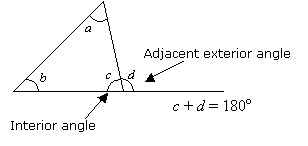
Property 2:

The sum of an interior angle and its adjacent exterior angle is 180°.

Example:

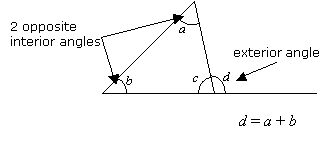
Property 3: Exterior Angle Theorem

An exterior angle of a triangle is equal to the sum of the two opposite interior angles.

Example:

Exterior Angles of a Triangle
Finding the Unknown Angle of a Triangle
Example:

1. Evaluate triangle abc, where a = 40° and b = 60°. What is the exterior angle to ∠acb?
   
2. Evaluate triangle abc, where a = 50° and b = 30°. What is the exterior angle to ∠acb?
   
3. Evaluate triangle abc, where a = 90° and b = 40°. What is the exterior angle to ∠acb?
   

• Show Step-by-step Solutions

How to use the Exterior Angle Theorem to solve problems involving angles in a triangle?

• Show Step-by-step Solutions

Property 4:

An equilateral triangle has 3 equal angles that are 60° each.
An isosceles triangle has 2 equal angles, which are the angles opposite the 2 equal sides.

How to Find the Missing Angle in an Isosceles Triangle?

• Show Step-by-step Solutions

Parallel Lines and the Triangle Angle-Sum Theorem

• Show Step-by-step Solutions

The above angle properties can help us to find unknown angles in a triangle.

Example:
Find the value of x in the following triangle.

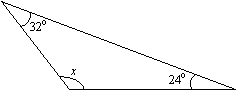
Solution:
x + 24° + 32° = 180° (sum of angles is 180°)
x + 56° = 180°
x = 180° – 56° = 124°

Example:
Find the values of x and y in the following triangle.

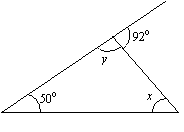
Solution:
x + 50° = 92° (sum of opposite interior angles = exterior angle)
x = 92° – 50° = 42°

y + 92° = 180° (interior angle + adjacent exterior angle = 180°.)
y = 180° – 92° = 88°

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.