Triangle Altitude
Related Topics:
More Lessons for Grade 9 Math
Math Worksheets
Videos, solutions, examples, worksheets, games and activities to help Geometry students learn how to construct the altitude of a triangle.
Altitude
Altitudes are defined as perpendicular line segments from the vertex to the line containing the opposite side.
In each triangle, there are three triangle altitudes, one from each vertex.
In an acute triangle, all altitudes lie within the triangle.
In a right triangle, the altitudes for two of the vertices are the sides of the triangle.
In an obtuse triangle, the altitudes meet outside of the triangle.
Orthocenter
The three altitude lines meet at a point called the Orthocenter.
In an acute triangle, the orthocenter lies within the triangle.
In a right triangle, the orthocenter coincides with the vertex of the right angle.
In an obtuse triangle, the orthocenter lies outside of the triangle.
The following diagrams show the altitudes and orthocenters for an acute triangle, right triangle and obtuse triangle.
Scroll down the page for more examples and solutions on how to construct the altitudes and orthocenter of a triangle.
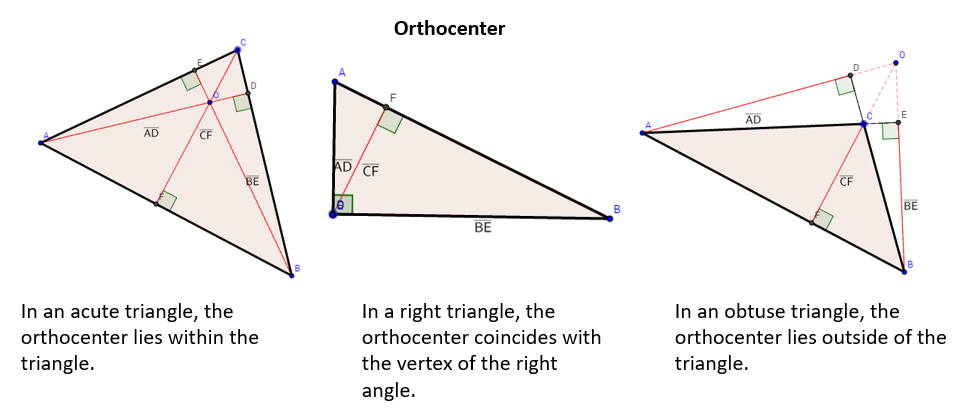
How to draw altitude lines in acute, right and obtuse triangles
Three altitude lines intersect at a common point called the orthocenter.
Constructing an altitude inside of the triangle
Using a compass and a straight edge to create the altitude of a triangle that lies inside the triangle.
Constructing an altitude outside the triangle
Using a straight edge and a compass to construct an altitude outside of the triangle How to Construct the Orthocenter of an Acute Triangle?
How to construct the orthocenter of an acute triangle using a compass and straightedge?
How to Construct the Orthocenter of an Obtuse Triangle?
How to construct the orthocenter of an obtuse triangle using a compass and straightedge?
More Lessons for Grade 9 Math
Math Worksheets
Videos, solutions, examples, worksheets, games and activities to help Geometry students learn how to construct the altitude of a triangle.
Altitude
Altitudes are defined as perpendicular line segments from the vertex to the line containing the opposite side.
In each triangle, there are three triangle altitudes, one from each vertex.
In an acute triangle, all altitudes lie within the triangle.
In a right triangle, the altitudes for two of the vertices are the sides of the triangle.
In an obtuse triangle, the altitudes meet outside of the triangle.
Orthocenter
The three altitude lines meet at a point called the Orthocenter.
In an acute triangle, the orthocenter lies within the triangle.
In a right triangle, the orthocenter coincides with the vertex of the right angle.
In an obtuse triangle, the orthocenter lies outside of the triangle.
The following diagrams show the altitudes and orthocenters for an acute triangle, right triangle and obtuse triangle.
Scroll down the page for more examples and solutions on how to construct the altitudes and orthocenter of a triangle.
How to draw altitude lines in acute, right and obtuse triangles
Three altitude lines intersect at a common point called the orthocenter.
Constructing an altitude inside of the triangle
Using a compass and a straight edge to create the altitude of a triangle that lies inside the triangle.
Using a straight edge and a compass to construct an altitude outside of the triangle How to Construct the Orthocenter of an Acute Triangle?
How to construct the orthocenter of an acute triangle using a compass and straightedge?
How to Construct the Orthocenter of an Obtuse Triangle?
How to construct the orthocenter of an obtuse triangle using a compass and straightedge?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.