Trapezium Rule

What is the Trapezium Rule?
The Trapezium Rule is a numerical method used to approximate the definite integral of a function. Since the definite integral represents the area under the curve of the function between two limits, the Trapezium Rule estimates this area by dividing it into several trapezoids and summing their areas.

Instead of using rectangles (as in Riemann sums) to approximate the area under a curve, the Trapezium Rule uses trapezoids. A trapezoid formed under a small segment of the curve will generally fit the shape of the curve more closely than a rectangle, leading to a more accurate approximation of the integral.

Graphically, the Trapezium Rule helps us to find the approximate area under the curve defined by the function.

The following diagram shows the Trapezium Rule to find an approximation to an integral between two limits. Scroll down the page for more examples and solutions on how to use the Trapezium Rule.

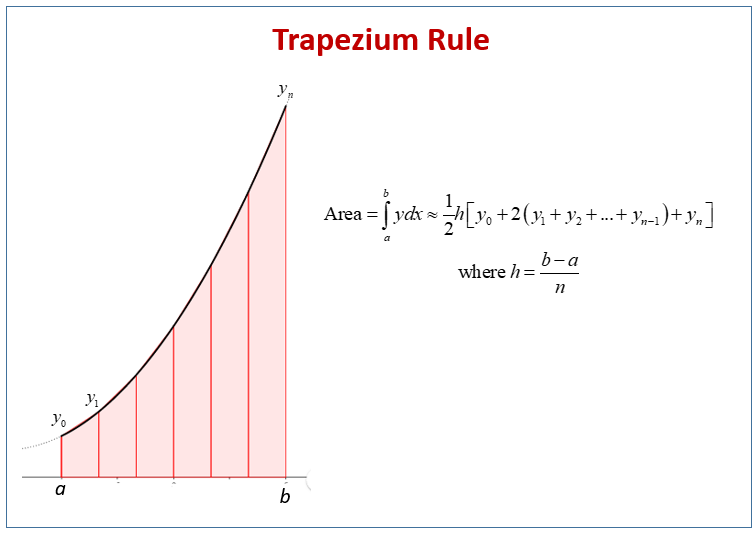
Steps to Apply the Trapezium Rule:

1. Determine the interval of integration:
   Identify the lower limit (a) and upper limit (b) of the integration. [a,b].
   
2. Choose the number of subintervals (n):
   A larger n generally leads to a more accurate approximation.
   
3. Calculate the width of each subinterval.
   Use the formula h=(b−a)/n.
   
4. Find the x-values of the points.
   Starting from x₀ = a, calculate x₁ = a + h, x₂ = a + 2h, and so on, up to x_n = b.
   
5. Calculate the corresponding y-values.
   For each x_i, find y_i = f(x_i).
   
6. Apply the Trapezium Rule formula.
   Substitute the values of h and the y-values into the Trapezium Rule formula.

The Trapezium Rule in 5 minutes

• Show Step-by-step Solutions

How to use the Trapezium Rule?
A short tutorial giving one example on using the trapezium rule to find an approximation to an integral.

• Show Step-by-step Solutions

A-Level Edexcel C4 January 2010 Q2(a-b)
Worked solution to this question on the integration by parts and the trapezium rule

• Show Step-by-step Solutions

A-Level Edexcel C4 January 2010 Q2c (i)
Worked solution to this question on the integration by parts and the trapezium rule.

• Show Step-by-step Solutions

A-Level Edexcel C4 January 2010 Q2c(ii)
Worked solution to this question on the integration by parts and the trapezium rule.

• Show Step-by-step Solutions

Accuracy and Error:
The accuracy of the Trapezium Rule depends on the number of subintervals used and the nature of the function. Generally:

• Increasing the number of subintervals (n) decreases the error and improves the accuracy.
• The Trapezium Rule provides an exact result if the function f(x) is linear.
• For functions with significant curvature (large second derivative), the Trapezium Rule may require a large number of subintervals to achieve a desired level of accuracy.

When to Use the Trapezium Rule

• Functions without elementary antiderivatives.
• Data points from experiments (no explicit function).
• Quick approximations where high precision isn’t critical.

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.