Illustrative Mathematics Grade 8, Unit 3, Lesson 8: Translating to y=mx+b

Related Pages
Illustrative Math
Grade 8

Lesson 8: Translating to y = mx + b

Let’s see what happens to the equations of translated lines.

Illustrative Math Unit 8.3, Lesson 8 (printable worksheets)

Lesson 8 Summary

The following diagram shows what happens to the equations of translated lines.

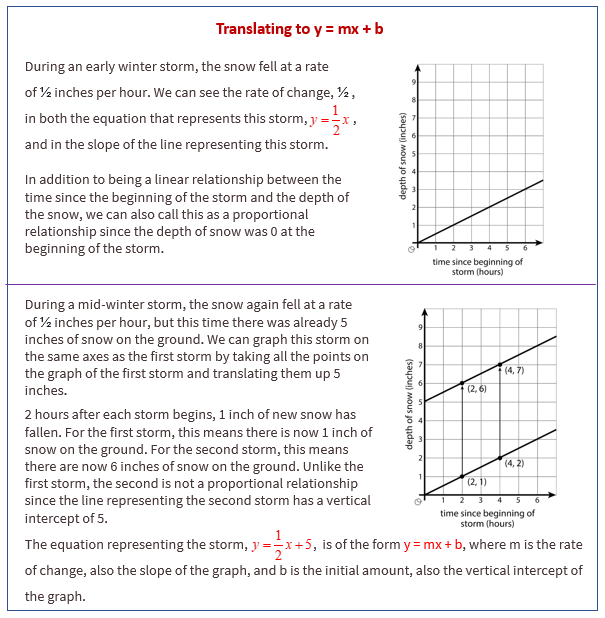
Lesson 8.1 Lines that Are Translations

The diagram shows several lines. You can only see part of the lines, but they actually continue forever in both directions.

1. Which lines are images of line f under a translation?
2. For each line that is a translation of f, draw an arrow on the grid that shows the vertical translation distance.

• See Video for Whole Lesson

Lesson 8.2 Increased Savings

Open Applet

1. Diego earns $10 per hour babysitting. Assume that he has no money saved before he starts babysitting and plans to save all of his earnings. Graph how much money, y, he has after x hours of babysitting.
2. Now imagine that Diego started with $30 saved before he starts babysitting. On the same set of axes, graph how much money, y, he would have after x hours of babysitting.
3. Compare the second line with the first line. How much more money does Diego have after 1 hour of babysitting? 2 hours? 5 hours? x hours?
4. Write an equation for each line.

Lesson 8.3 Translating a Line

Open Applet

1. Experiment with moving point A.
   a. Place point A in three different locations above the x-axis. For each location, write the equation of the line and the coordinates of point A.
   b. Place point A in three different locations below the x-axis. For each location, write the equation of the line and the coordinates of point A.
   c. In the equations, what changes as you move the line? What stays the same?
   d. If the line passes through the origin, what equation is displayed? Why do you think this is the case?
2. Your teacher will give you 12 cards. There are 4 pairs of lines, A–D, showing the graph, a, of a proportional relationship and the image, h, of a under a translation. Match each line h with an equation and either a table or description. For the line with no matching equation, write one on the blank card.

Are you ready for more?

A student says that the graph of the equation y = 3(x + 8) is the same as the graph of y = 3x, only translated upwards by 8 units. Do you agree? Why or why not?

• Show Answers

  y = 3(x + 8) = 3x + 24
  y = 3(x + 8) is the same as the graph of y = 3x, but translated upwards by 24 units

Lesson 8 Practice Problems

1. Select all equations that have graphs with the same y-intercept.
2. Create a graph showing the equations y = 1/4 x and y = 1/4 x - 5. Explain how the graphs are the same and how they are different.
3. A cable company charges $70 per month for cable service to existing customers.
   a. Find a linear equation representing the relationship between x, the number of months of service, and y, the total amount paid in dollars by an existing customer.
   b. For new customers, there is an additional one-time $100 service fee. Repeat the previous problem for new customers.
   c. When the two equations are graphed in the coordinate plane, how are they related to each other geometrically?
4. Match each graph to a situation.
5. A mountain road is 5 miles long and gains elevation at a constant rate. After 2 miles, the elevation is 5500 feet above sea level. After 4 miles, the elevation is 6200 feet above sea level.
   a. Find the elevation of the road at the point where the road begins.
   b. Describe where you would see the point in part (a) on a graph where represents the elevation in feet and x represents the distance along the road in miles.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.