Transformations Of Linear Functions

Related Pages
Graphs Of Functions
Parent Functions And Their Graphs
Transformations Of Graphs
More Pre-Calculus Lessons

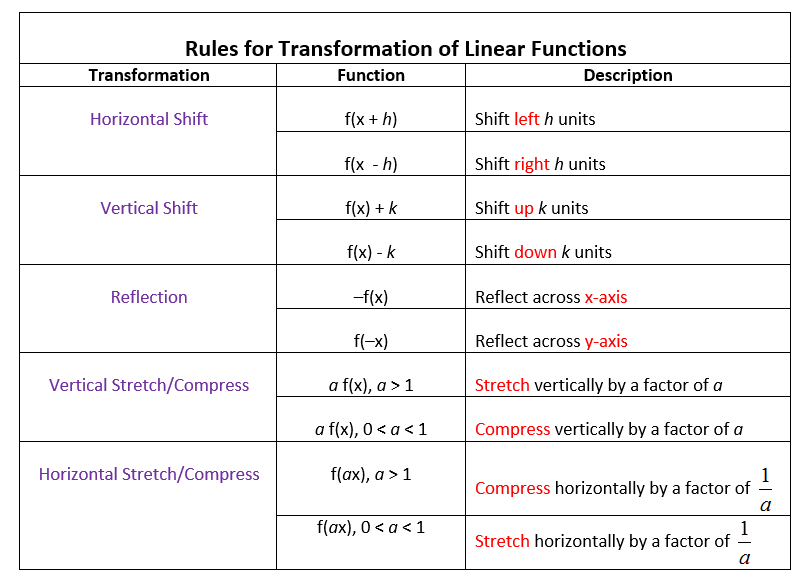
Rules For Transformation Of Linear Functions

The following table gives the rules for the transformation of linear functions. Scroll down the page if you need more explanations about the rules and examples on how to use the rules.

How To Transform Linear Functions?

Transforming Linear Functions (Shift And Reflection)

Horizontal shift of |h| units
• f(x) → f(x - h)
• h > 0 moves right, h < 0 moves left

Vertical shift of |k| units
• f(x) → f(x) + k
• k > 0 moves up, k < 0 moves down

Reflection across y-axis
• f(x) → f(-x)
• The lines are symmetric about the y-axis

Reflection across x-axis
• f(x) → -f(x)
• The lines are symmetric about the x-axis

Examples:

1. Let g(x) be the indicated transformation of f(x). Write the rule for g(x).
   a) f(x) = x - 2; horizontal translation right 3 units.
   b) f(x) = 3x + 1; translation 2 units right.
2. Let g(x) be a reflection over the x-axis of f(x). Write the rule for g(x).

• Show Video Lesson

Transforming Linear Functions (Stretch And Compression)

Stretches and compressions change the slope of a linear function.
If the line becomes steeper, the function has been stretched vertically or compressed horizontally.
If the line becomes flatter, the function has been stretched horizontally or compressed vertically.

Horizontal Stretch/Compression by a factor of b
• \(f\left( x \right) \to f\left( {\frac{1}{b}x} \right)\) • b > 1 stretches away from the y-axis.
• 0 < |b| < 1 compresses toward the y-axis.
• y-intercepts remain the same.

Vertical Stretch/Compression by a factor of a
• f(x) → af(x) • a > 1 stretches away from the x-axis.
• 0 < |a| < 1 compresses toward the x-axis.
• x-intercepts remain the same.

Examples:

1. Let g(x) be a horizontal compression of f(x) = -x + 4 by a factor of 1/2. Write the rule for g(x), and graph the function.
2. Let g(x) be a horizontal compression of f(x) = 3x + 2 by a factor of 1/4. Write the rule for g(x), and graph the function.
3. Let g(x) be a horizontal shift of f(x) = 3x, left 6 units followed by a horizontal stretch by a factor of 4. Write the rule for g(x).

• Show Video Lesson

Transformations Of Linear Functions

Learn how to modify the equation of a linear function to shift (translate) the graph up, down, left, or right.
Learn how to reflect the graph over an axis. And how to narrow or widen the graph.

Examples:
y = f(x) + 1
y = f(x - 2)
y = -2f(x)

• Show Video Lesson

Linear Parent Graph And Transformations

Students learn that the linear equation y = x, or the diagonal line that passes through the origin, is called the parent graph for the family of linear equations.

Students also learn the different types of transformations of the linear parent graph. For example, if the parent graph is shifted up or down (y = x + 3), the transformation is called a translation.

If the parent graph is made steeper or less steep (y = ½ x), the transformation is called a dilation.

And if the parent graph is changed so that it falls to the right instead of rising to the right (y = -x), the transformation is called a reflection.

Example:
Compare the graph of each of the following equations with the graph of y = x, and determine if it represents a translation, dilation, or reflection.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.