Illustrative Mathematics Unit 6.1, Lesson 1: Tiling the Plane

Related Pages
Math Worksheets

Return to the list of Illustrative Math lessons

Tiling the Plane
Let’s look at tiling patterns and think about area.

Illustrative Math Unit 6.1, Lesson 1 (printable worksheets)

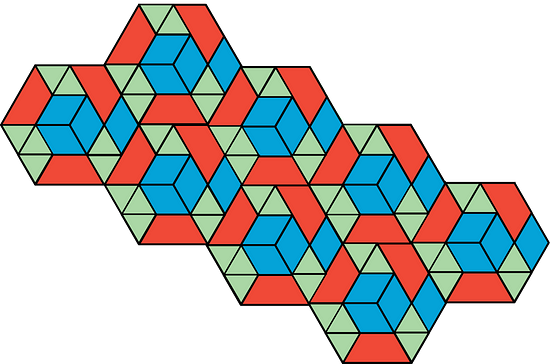
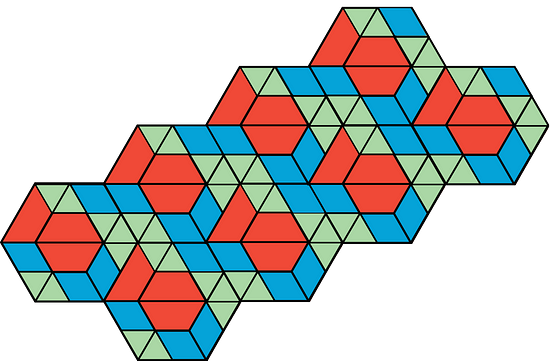
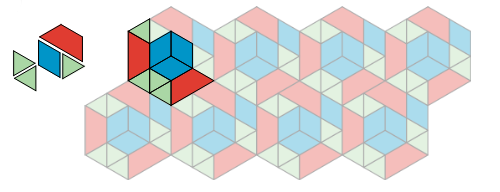
1.1 - Which One Doesn’t Belong: Tilings

Which pattern doesn’t belong? Give reasons.

• What is Tiling the Plane?

  Tiling the plane means covering a two-dimensional region with copies of the same shape or shapes so that there are no gaps or overlaps. Which patterns are examples of tiling and which are not?

• See Possible Answers

  In terms of appearance, all of the patterns are different from every other pattern in some way. For example:

  • Pattern A does not have any yellow.
  • Pattern B does not have any blue.
  • Pattern C does not have any five-sided shapes.
  • Pattern D has irregular white spaces or shapes.

  These are examples; any one of these patterns might not belong, for other reasons you might think of.

  In terms of tiling the plane, Pattern A, Pattern B, and Pattern C are examples of tiling, while Pattern D is not because of the irregular white spaces.

• See Video 1 for Whole Lesson
• See Video 2 for Whole Lesson

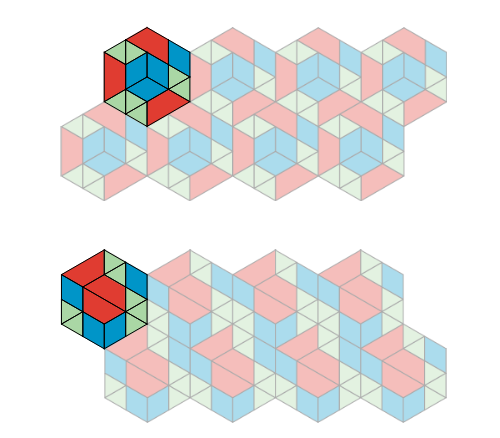
1.2 - More Red, Green, or Blue?

Look at Pattern A or B.

In your pattern, which shapes cover more of the plane: blue rhombuses, red trapezoids, or green triangles? Explain how you know.

• Show Pattern A
  
• Show Pattern B
  

You may use the applet here to help.

• Hints

  Notice how the pattern is repeated. Do you need to count all the shapes in the pattern?

  
  
  The shapes are different sizes. So is counting them enough? Compare the area covered by each type of shape in the pattern. How many triangles match up to one rhombus? How about trapezoids?

  
  
  Can you then compare the area covered by all the triangles in the pattern with the area covered by all the rhombuses, or all the trapezoids?

• Answers

  “Which shapes cover more of the plane” means that we are comparing the areas covered by the different types of shapes. In these patterns, two triangles match up to one rhombus, and three triangles match up to one trapezoid.

  In both Pattern A and Pattern B, the first hexagonal part is made up of 7 triangles, 4 rhombuses, and 3 trapezoids.

  The first hexagonal part is repeated across the pattern, so whichever type of shape covers the most area of this first part also covers the most area in the whole pattern.

  Since the triangles can be matched to the other shapes, let us say 1 triangle is 1 space, or 1 unit of area, in the pattern. So the 7 triangles cover 7 spaces.

  As each rhombus is 2 triangles, rhombuses cover 4 × 2 = 8 spaces.

  The trapezoids cover 3 × 3 = 9 spaces.

  Hence, red trapezoids cover more of the plane in both Pattern A and Pattern B.

Lesson 1 Summary

In this lesson, we learned about tiling the plane, which means covering a two-dimensional region with copies of the same shape or shapes such that there are no gaps or overlaps.

Then, we compared tiling patterns and the shapes in them. In thinking about which patterns and shapes cover more of the plane, we have started to reason about area.

We will continue this work, and to learn how to use mathematical tools strategically.

Practice Problems

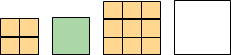
1. Which square—large, medium, or small—covers more of the plane? Explain your reasoning.

• Show Diagram
  
• Answers
  

  The pattern is repeated, so whichever type of square covers the most area of the first part also covers the most area in the whole pattern.

  

  1 small square is 1 space, or 1 unit of area, in the pattern. 2 small squares are 2 spaces.

  The medium squares cover 2 × 4 = 8 spaces.

  The large square covers 3 × 3 = 9 spaces.

  Hence, the large squares cover more of the plane compared to the other squares.

2. Draw three different quadrilaterals, each with an area of 12 square units. (The grid is 10 units tall and 16 units wide.)

• Show Grid
  
• See Possible Answers
  

  These are examples of quadrilaterals that have an area of 12 square units. Any three quadrilaterals which enclose 12 square units are valid. Notice that the sloping sides of the trapezium can form triangles which enclose half a square unit each.

3. Use copies of the rectangle to show how a rectangle could:
   a. tile the plane.
   b. not tile the plane.

• Show Diagram
  
• See Possible Answers

  
  
  The blue rectangles on the left-hand grid tile the grid. The blue rectangles on the right-hand grid do not tile the grid, since there are gaps and overlaps.

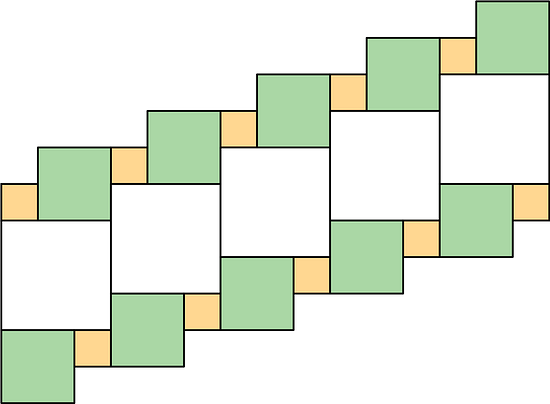
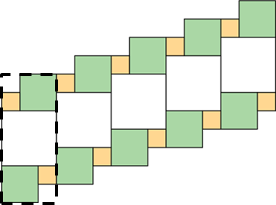
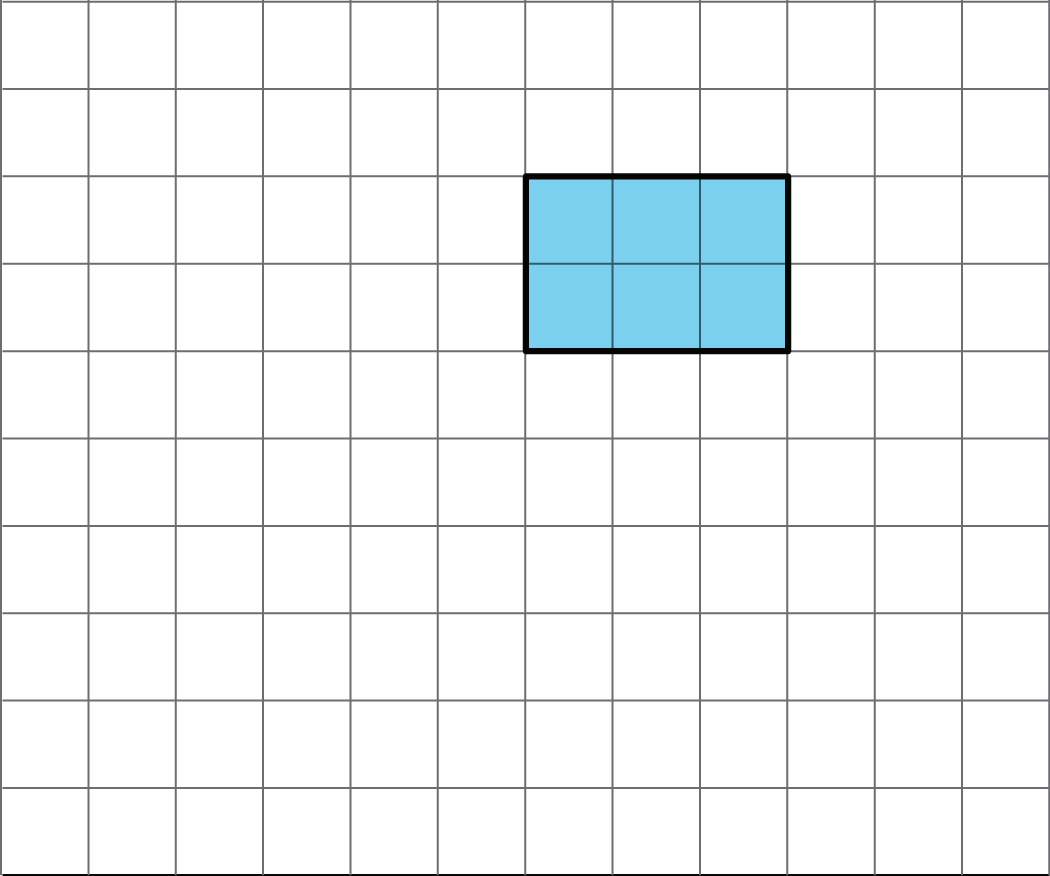
4. The area of this shape is 24 square units. Which of the statements below is true about the area? Select all that apply.
   

• Show Shape
  A: The area can be found by counting the number of squares that touch the edge of the shape.
  B: It takes 24 grid squares to cover the shape without gaps and overlaps.
  C: The area can be found by multiplying the side lengths that are 6 units and 4 units.
  D: The area can be found by counting the grid squares inside the shape.
  E: The area can be found by adding 4 × 3 and 6 × 2.
• Answers

  A: False. The area of the shape is the area covered or enclosed by the whole shape, not only its edges.
  B: True. The area of the shape is 24 square units, the same as 24 grid squares.
  C: Multiplying the side lengths is the formula for finding the area of a rectangle. The shape as presented is irregular. However, the 24 square units of this shape can be rearranged to create a rectangle which is 6 units by 4 units.
  D: True. The area of a shape is the area inside a shape.
  E: True. The shape can be broken down into two rectangles 4 × 3 units and 6 × 2 units, whose areas can be added together to find the area of the whole shape.

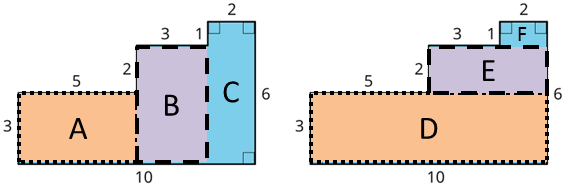
5. Show two different ways for finding the area of the shaded region. All angles are right angles.
   

• Show Shape
  
• See Possible Answers

  
  
  The figure can be divided into 3 rectangles.
  On the left, rectangle A is 3 units tall × 5 units wide, rectangle B is (3 + 2) units tall × 3 units wide, and rectangle C is 6 units tall × 2 units wide. The total area is (3×5)+(5×3)+(6×2) = 42 units.
  On the right, rectangle D is 3 units tall × 10 units wide, rectangle E is 2 units tall × (3 + 2) units wide, and rectangle F is 1 unit tall × 2 units wide. The total area is (3×10)+(2×5)+(1×2) = 42 units.
  Other ways of subdividing or rearranging the figure may also give the same answer of 42 units.

6. Which shape has a larger area: a rectangle that is 7 inches by ¾ inch, or a square with a side length of 2½ inches? Show your reasoning.

• Answers

  To find the area of a rectangle or square, multiply the side lengths.
  The area of the rectangle is 7 × ¾ = 5¼ square inches.
  The area of the square is 2½ × 2½ = 6¼ square inches.
  Therefore, the square has the larger area.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.