Theorems involving Trapezoids

Related Pages
More Lessons for High School Regents Exam
Math Worksheets

The following diagram shows some theorems for rectangles, rhombuses, and squares. Scroll down the page for more examples and solutions on postulates and theorems for rectangles, rhombuses, and squares.

 

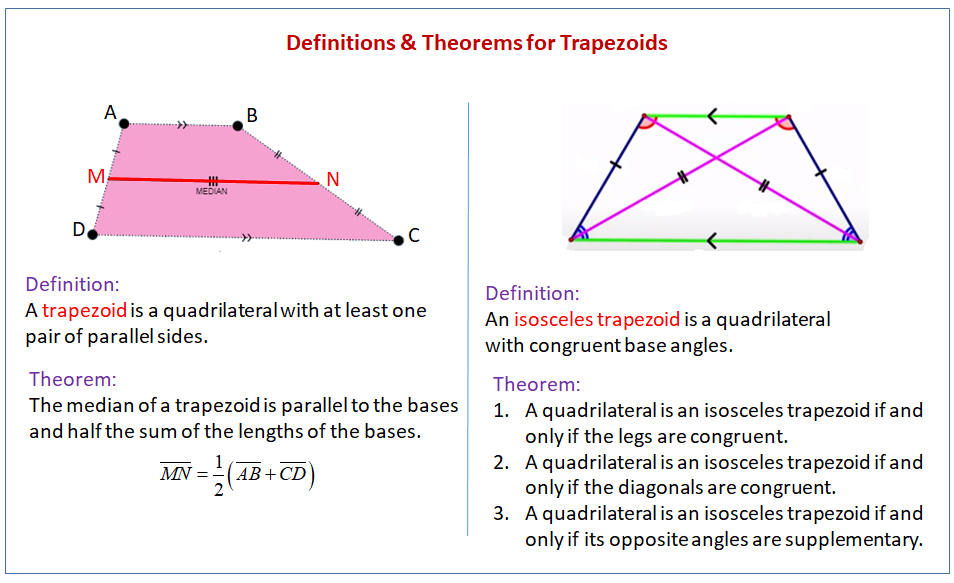
Trapezoid and Kite Theorems & Corollaries

Theorems:

1. Midsegment Theorem for Trapezoids
   The midsegment of a trapezoid is parallel to each base and its length is one half the sum of the lengths of the bases (average of the bases)

2. If a trapezoid is isosceles, then each pair of base angles is congruent.
   

3. If a trapezoid has a pair of congruent base angles, then it is an isosceles trapezoid.
   

4. A trapezoid is isosceles if and only if its diagonals are congruent.

5. If a quadrilateral is a kite, then its diagonals are perpendicular.
   

6. If a quadrilateral is a kite, then exactly one pair of opposite angles are congruent.

• Show Step-by-step Explanations

Isosceles Trapezoid Theorem

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.