

Theorems involving Rectangles, Rhombuses & Squares
Related Topics:
More Lessons for High School Regents Exam
Math Worksheets
High School Math based on the topics required for the Regents Exam conducted by NYSED.
Rhombus Corollary and Theorems
A quadrilateral is a rhombus if and only if it has four congruent sides.
Theorem
A parallelogram is a rhombus if and only if its diagonals are perpendicular.
Theorem
A parallelogram is a rhombus if and only if each diagonal bisects a pair of opposite angles.
Rectangle Corollary and Theorem
A quadrilateral is a rectangle if and only if it has four right angles.
Theorem
A parallelogram is a rectangle if and only if its diagonals are congruent.
Square Corollary
A quadrilateral is a square if and only if it is a rhombus and a rectangle.
Conditions for Rectangles, Rhombuses, and Squares



More Lessons for High School Regents Exam
Math Worksheets
High School Math based on the topics required for the Regents Exam conducted by NYSED.
The following diagram shows some theorems for rectangles, rhombuses, and squares. Scroll down the page for more examples and solutions on postulates and theorems for rectangles, rhombuses, and squares.
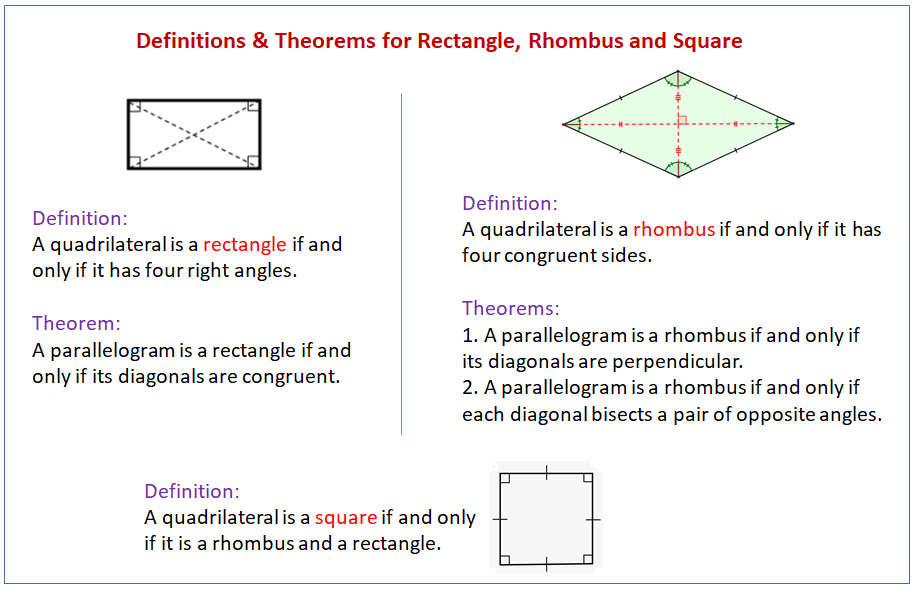
Rhombus Corollary and Theorems
A quadrilateral is a rhombus if and only if it has four congruent sides.
Theorem
A parallelogram is a rhombus if and only if its diagonals are perpendicular.
Theorem
A parallelogram is a rhombus if and only if each diagonal bisects a pair of opposite angles.
Rectangle Corollary and Theorem
A quadrilateral is a rectangle if and only if it has four right angles.
Theorem
A parallelogram is a rectangle if and only if its diagonals are congruent.
Square Corollary
A quadrilateral is a square if and only if it is a rhombus and a rectangle.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.