

Fundamental Theorem of Calculus
More Lessons for Calculus
Math Worksheets
In this lesson, we introduce the Fundamental Theorem of Calculus.
What is the Fundamental Theorem of Calculus?
The Fundamental Theorem of Calculus, Part 1
If f is continuous on [a, b], then the function g is defined by
![]()
is continuous on [a, b] and differentiable on (a, b), and g'(x) = f(x)
The Fundamental Theorem of Calculus, Part 2
If f is continuous on [a, b], then
where F is any antiderivative of f, that is, a function such that F ’ = f
Example:
Find the area under the parabola y = x2 from 0 to 1.
Solution:
An antiderivative of f (x) = x2 is ![]()
Use Part 2 of the Fundamental Theorem to find the required area A.
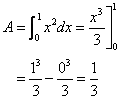
The fundamental theorem of Calculus is an important theorem relating antiderivatives and definite integrals in Calculus. The fundamental theorem of Calculus states that if a function f has an antiderivative F, then the definite integral of f from a to b is equal to F(b)-F(a). This theorem is useful for finding the net change, area, or average value of a function over a region.
The Fundamental Theorem of Calculus Part 1
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.