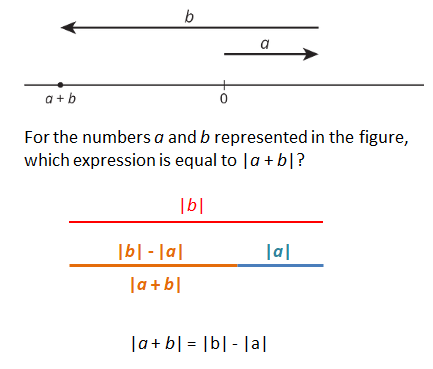Illustrative Mathematics Grade 7, Unit 5, Lesson 2: Changing Temperatures

Related Pages
Illustrative Math
Grade 7

Lesson 2: Changing Temperatures

Let’s add signed numbers.

Illustrative Math Unit 7.5, Lesson 2 (printable worksheets)

Lesson 2 Summary

The following diagram shows how to relate signed numbers to changing temperatures and how to use a number line to add positive and negative numbers.

Lesson 2.1 Which One Doesn’t Belong: Arrows

Which pair of arrows doesn’t belong?

• See Video for Whole Lesson

Lesson 2.2 Warmer and Colder

1. Complete the table and draw a number line diagram for each situation.
2. Complete the table and draw a number line diagram for each situation.

Are you ready for more?

For the numbers a and b represented in the figure, which expression is equal to |a + b|?

• Show Answer

  

Lesson 2.3 Winter Temperatures

1. One winter day, the temperature in Houston is 8° Celsius. Find the temperatures in these other cities. Explain or show your reasoning.
   a. In Orlando, it is warmer than it is in Houston.
   b. In Salt Lake City, it is colder than it is in Houston.
   c. In Minneapolis, it is colder than it is in Houston.
   
2. In Fairbanks, it is colder than it is in Minneapolis. What is the temperature in Fairbanks?
3. Use the thermometer applet to verify your answers and explore your own scenarios. See Applet

Lesson 2 Practice Problems

1. a. The temperature is -2°C. If the temperature rises by 15°C, what is the new temperature?
   b. At midnight the temperature is -6°C. At midday the temperature is 9°C. By how much did the temperature rise?
   
2. Complete each statement with a number that makes the statement true.
   
3. Draw a diagram to represent each of these situations. Then write an addition expression that represents the final temperature.
   a. The temperature was 80°F and then fell 20°F.
   b. The temperature was -13°F and then rose 9°F.
   c. The temperature was -5°F and then fell 8°F.
   
4. Decide whether each table could represent a proportional relationship. If the relationship could be proportional, what would be the constant of proportionality?
   a. The number of wheels on a group of buses.
   b. The number of wheels on a train.
   
5. Noah was assigned to make 64 cookies for the bake sale. He made 125% of that number. 90% of the cookies he made were sold. How many of Noah’s cookies were left after the bake sale?

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.