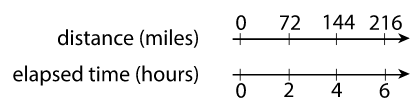Illustrative Mathematics Unit 6.2, Lesson 13: Tables and Double Number Line Diagrams
Learning Targets:
- I can create a table that represents a set of equivalent ratios.
- I can explain why sometimes a table is easier to use than a double number line to solve problems involving equivalent ratios.
- I include column labels when I create a table, so that the meaning of the numbers is clear.
Related Pages
Illustrative Math
Grade 6
Lesson 13: Tables and Double Number Line Diagrams
Let’s contrast double number lines and tables.
Illustrative Math Unit 6.2, Lesson 13 (printable worksheets)
Lesson 13 Summary
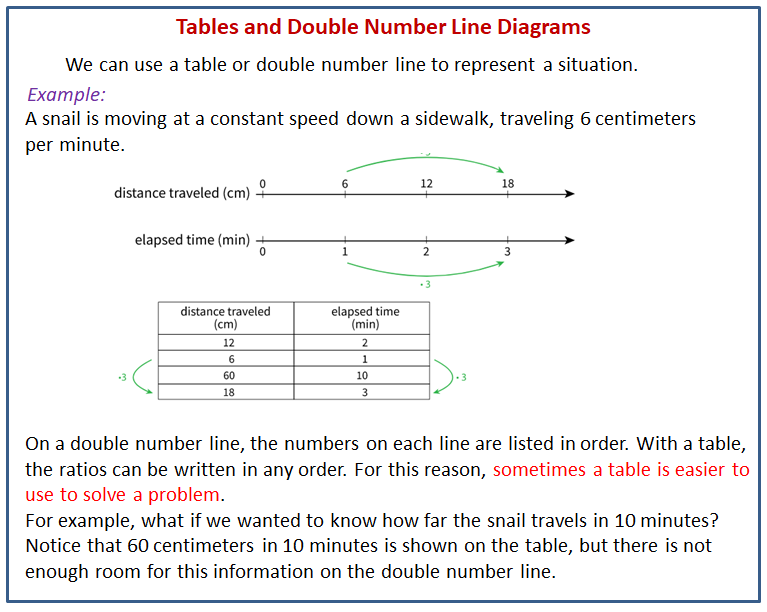
The following diagram shows how to use a table or a double number line to represent a situation.
13.1 Number Talk: Constant Dividend
-
Find the product mentally.
150 ÷ 2
150 ÷ 4
150 ÷ 8 -
Locate and label the quotients on the number line.
13.2 - Moving 3,000 Meters
The other day, we saw that Han can run 100 meters in 20 seconds.
Han wonders how long it would take him to run 3,000 meters at this rate. He made a table of equivalent ratios.
- Do you agree that this table represents the situation? Explain your reasoning.
- Complete the last row with the missing number.
- What question about the situation does this number answer?
- What could Han do to improve his table?
| 20 | 10 |
| 10 | 50 |
| 1 | 5 |
| 3,000 |
- Priya can bike 150 meters in 20 seconds. At this rate, how long would it take her to bike 3,000 meters?
- Priya’s neighbor has a dirt bike that can go 360 meters in 15 seconds. At this rate, how long would it take them to ride 3,000 meters?
13.3 - The International Space Station
The International Space Station orbits around the Earth at a constant speed. Your teacher will give you either a double number line or a table that represents this situation. Your partner will get the other representation.
- Complete the parts of your representation that you can figure out for sure.
- Share information with your partner, and use the information that your partner shares to complete your representation.
- What is the speed of the International Space Station?
- Place the two completed representations side by side. Discuss with your partner some ways in which they are the same and some ways in which they are different.
- Record at least one way that they are the same and one way they are different.
Are you ready for more?
The Earth’s circumference is about 40,000 kilometers and the orbit of the International Space Station is just a bit more than this. About how long does it take for the International Space Station to orbit the Earth?
-
Show Answer
The speed of the International Space Station is approximately 8 km/s.
The distance of the orbit is approximately 40,000 km.
The time taken for one orbit is 40,000 ÷ 8 = 5000 seconds.
5000 seconds = 5000/60 minutes which is approximately 84 minutes (rounded up since the orbit is bigger than the circumference of the earth)
Lesson 13 Practice Problems
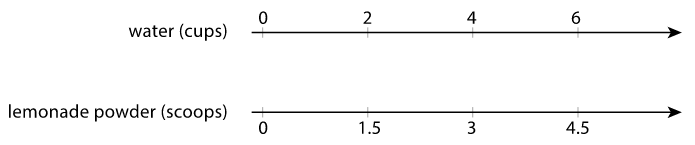
- The double number line shows how much water and how much lemonade powder to mix to make different amounts of lemonade.
Make a table that represents the same situation.
- A bread recipe uses 3 tablespoons of olive oil for every 2 cloves of crushed garlic.
a. Complete the table to show different-sized batches of bread that taste the same as the recipe.
b. Draw a double number line that represents the same situation.
c. Which representation do you think works better in this situation? Explain why.
| olive oil (tablespoons) | crushed garlic (cloves) |
| 3 | 2 |
| 1 | 1 |
| 2 | 11 |
| 5 | 11 |
| 10 | 11 |
- Clare travels at a constant speed, as shown on the double number line.
At this rate, how far does she travel in each of these intervals of time? Explain or show your reasoning. If you get stuck, consider using a table.
a. 1 hour
b. 3 hours
c. 6.5 hours
4. Lin and Diego travel in cars on the highway at constant speeds. In each case, decide who was traveling faster and explain how you know.
a. During the first half hour, Lin travels 23 miles while Diego travels 25 miles.
b. After stopping for lunch, they travel at different speeds. To travel the next 60 miles, it takes Lin 65 minutes and it takes Diego 70 minutes.
5. A sports drink recipe calls for 5/3 tablespoons of powdered drink mix for every 12 ounces of water. How many batches can you make with 5 tablespoons of drink mix and 36 ounces of water? Explain your reasoning.
6. In this cube, each small square has side length 1 unit.
What is the volume of this cube?
The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.