Illustrative Mathematics Grade 8, Unit 4, Lesson 12: Systems of Equations

Related Pages
Illustrative Math
Grade 8

Lesson 12: Systems of Equations

Let’s learn what a system of equations is.

Illustrative Math Unit 8.4, Lesson 12 (printable worksheets)

Lesson 12 Summary

The following diagram show how to make graphs to find an ordered pair that two real-world situations have in common.

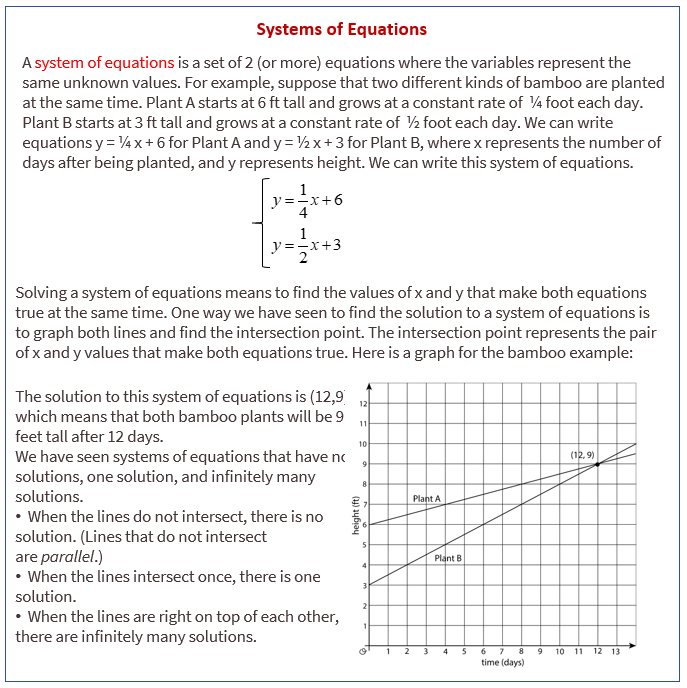
In future lessons, we will see that some systems cannot be easily solved by graphing, but can be easily solved using algebra.

Lesson 12.1 Milkshakes

Diego and Lin are drinking milkshakes. Lin starts with 12 ounces and drinks 1/4 an ounce per second. Diego starts with 20 ounces and drinks 2/3 an ounce per second.

1. How long will it take Lin and Diego to finish their milkshakes?
2. Without graphing, explain what the graphs in this situation would look like. Think about slope, intercepts, axis labels, units, and intersection points to guide your thinking.
3. Discuss your description with your partner. If you disagree, work to reach an agreement.

• See Video for Whole Lesson

Lesson 12.2 Bugs Passing in the Night, Continued

There is a hiking trail near the town where Han and Jada live that starts at a parking lot and ends at a lake. Han and Jada both decide to hike from the parking lot to the lake and back, but they start their hikes at different times.
At the time that Han reaches the lake and starts to turn back, Jada is 0.6 miles away from the parking lot and hiking at a constant speed of 3.2 miles per hour toward the lake. Han’s distance, d, from the parking lot can be expressed as d = -2.4t + 4.8, where represents the time in hours since he left the lake.

1. What is an equation for Jada’s distance from the parking lot as she heads toward the lake?
2. Draw both graphs: one representing Han’s equation and one representing Jada’s equation. It is important to be very precise. Open Applet
3. Find the point where the two graphs intersect each other. What are the coordinates of this point?
4. What do the coordinates mean in this situation?
5. What has to be true about the relationship between these coordinates and Jada’s equation?
6. What has to be true about the relationship between these coordinates and Han’s equation?

Lesson 12.3 Stacks of Cups

A stack of n small cups has a height, h, in centimeters of h = 1.5n + 6. A stack of n large cups has a height,h , in centimeters of h = 1.5n + 9.

1. Graph the equations for each cup on the same set of axes. Make sure to label the axes and decide on an appropriate scale. Open Applet
2. For what number of cups will the two stacks have the same height?

Lesson 12 Practice Problems

1. Here is the graph for one equation in a system of equations:
   a. Write a second equation for the system so it has infinitely many solutions.
   b. Write a second equation whose graph goes through (0,1) so the system has no solutions.
   c. Write a second equation whose graph goes through (0,2) so the system has one solution at 4,1).
2. Create a second equation so the system has no solutions.
3. Andre is in charge of cooking broccoli and zucchini for a large group. He has to spend all $17 he has and can carry 10 pounds of veggies. Zucchini costs $1.50 per pound and broccoli costs $2 per pound. One graph shows combinations of zucchini and broccoli that weigh 10 pounds and the other shows combinations of zucchini and broccoli that cost $17.
   a. Name one combination of veggies that weighs 10 pounds but does not cost $17.
   b. Name one combination of veggies that costs $17 but does not weigh 10 pounds.
   c. How many pounds each of zucchini and broccoli can Andre get so that he spends all $17 and gets 10 pounds of veggies?
4. The temperature in degrees Fahrenheit, F, is related to the temperature in degrees Celsius, C, by the equation
   a. In the Sahara desert, temperatures often reach 50 degrees Celsius. How many degrees Fahrenheit is this?
   b. In parts of Alaska, the temperatures can reach -60 degrees Fahrenheit. How many degrees Celsius is this?
   c. There is one temperature where the degrees Fahrenheit and degrees Celsius are the same, so that C = F. Use the expression from the equation, where F is expressed in terms of C, to solve for this temperature.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.