Synthetic Division

What is Synthetic Division?

Synthetic Division is an abbreviated way of dividing a polynomial by a binomial of the form (x + c) or (x – c). We can simplify the division by detaching the coefficients.

The following diagrams show how to divide polynomials using synthetic division. Scroll down the page for more examples and solutions.

 

• Printable & Online Polynomial Worksheets

  Add & Subtract Polynomials
  Multiply Polynomials
  Divide Polynomials
  

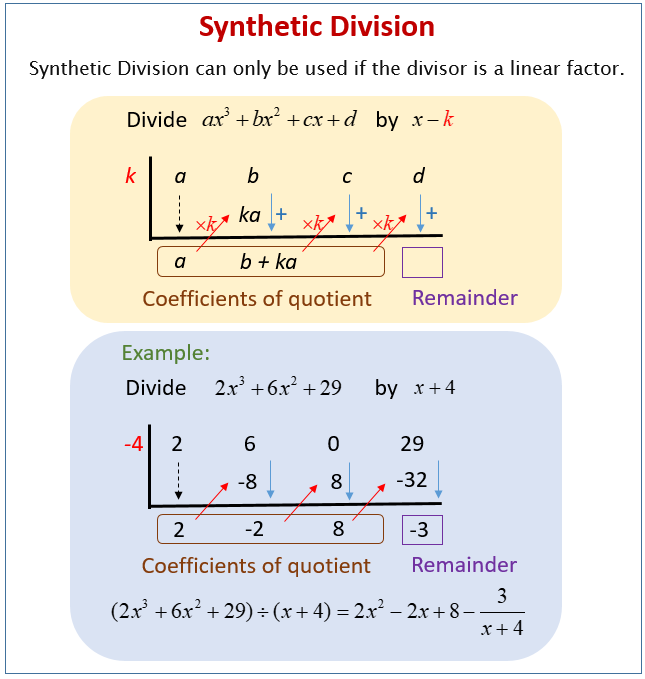
Example:
Evaluate (x³ – 8x + 3) ÷ (x + 3) using synthetic division

Solution:
(x³– 8x + 3) is called the dividend and (x + 3) is called the divisor.

Step 1: Write down the constant of the divisor with the sign changed
–3

Step 2: Write down the coefficients of the dividend. (Remember to add a coefficient of 0 for the missing terms)

 

Step 3: Bring down the first coefficient.

 

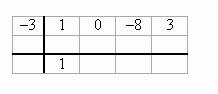
Step 4: Multiply (1)( –3) = –3 and add to the next coefficient.

 

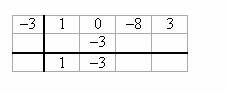
Repeat Step 4 for all the coefficients

 

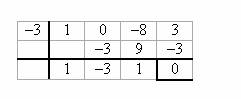
We find that (x³– 8x + 3) ÷ (x + 3) = x² – 3x + 1

Key Points to Remember

1. Synthetic division works only for divisors of the form x − c.
2. If the polynomial has missing terms, include 0 as their coefficients.
3. The last number is the remainder, and the other numbers are the coefficients of the quotient.

Videos

It is easier to learn Synthetic Division visually. Please watch the following videos for more examples of Synthetic Division.

Polynomial Division: Synthetic Division
Perform synthetic division to divide by a binomial in the form (x - k)

Example:
Divide using synthetic division

1. (2x³ + 6x² + 29) ÷ (x + 3)

2. (2x³ + 6x² - 17x + 15) ÷ (x + 5)

3. (y⁵ - 32) ÷ (y - 2)

4. (16x³ - 2 + 14x - 12x²) ÷ (2x + 1)

• Show Video Lesson

Divide a Trinomial by a Binomial Using Synthetic Division

Example:
Divide using synthetic division

1. (x² - 5x + 7) ÷ (x - 2)

2. (x² + 8x + 12) ÷ (x + 2)

• Show Video Lesson

Synthetic Division This video shows how you can use synthetic division to divide a polynomial by a linear expression.
It also shows how synthetic division can be used to evaluate polynomials.

Example:
(x³ - 2x² + 3x - 4) ÷ (x - 2)

• Show Video Lesson

Synthetic Division
This video shows how to use synthetic division to divide a polynomial by a linear expression and also how to use the remainder to evaluate the polynomial.

Example:
(x⁴ - x² + 5) ÷ (x + 3)

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.