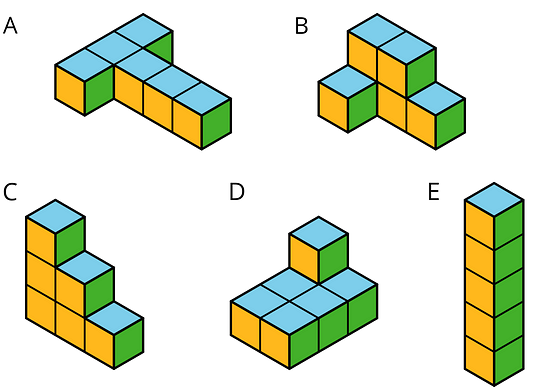OML Search

Illustrative Mathematics Unit 6.1, Lesson 16: Distinguishing Between Surface Area and Volume

Related Topics:
Math Worksheets




Learn more about the contrast between surface area and volume of three-dimensional shapes, and about the differences between one-, two-, and three-dimensional measurements and units. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons


Distinguishing Between Surface Area and Volume
Let’s contrast surface area and volume.

Illustrative Math Unit 6.1, Lesson 16 (printable worksheets)

16.1 - Attributes and Their Measures

For each quantity, choose one or more appropriate units of measurement.

For the last two rows, think of a quantity that could be appropriately measured with the given units.

Quantities:

  1. Perimeter of a parking lot:
  2. Volume of a semi truck:
  3. Surface area of a refrigerator:
  4. Length of an eyelash:
  5. Area of a state:
  6. Volume of an ocean:
  7. ______________________________: miles
  8. ______________________________: cubic meters

Units:

  • millimeters (mm)
  • feet (ft)
  • meters (m)
  • square inches (sq in)
  • square feet (sq ft)
  • square miles (sq mi)
  • cubic kilometers (cu km)
  • cubic yards (cu yd)

  • Answers
    1. Perimeter of a parking lot: feet or meters
    2. Volume of a semi truck: cubic yards
    3. Surface area of a refrigerator: square inches
    4. Length of an eyelash: millimeters
    5. Area of a state: square miles
    6. Volume of an ocean: cubic kilometers
    7. Length of a highway: miles
    8. Volume of a swimming pool: cubic meters

    Area is always measured in square units and volume is always measured in cubic units.

  • See Video 1 for Whole Lesson
  • See Video 2 for Whole Lesson




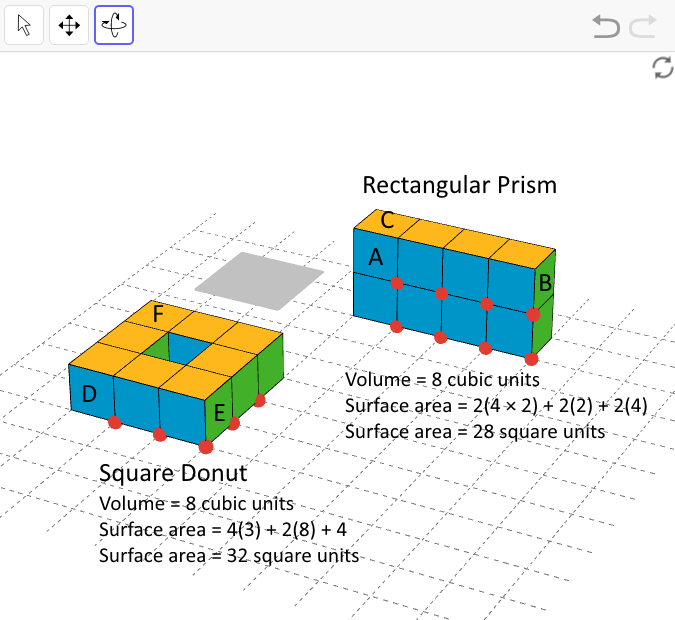
16.2 - Building with 8 Cubes

Open the applet. Drag on the red point on the cube to move it, and click on the point to switch between vertical and horizontal movement. The gray square will give you 16 cubes. Build 2 different shapes using 8 cubes for each.

For each shape, determine the following information and write it down:
Give a name or a label (e.g., Mae’s First Shape or Eric’s Steps).
Determine its volume.
Determine its surface area.

  • Hints

    You may create prisms or non-prisms. You can find the surface area or volume of any shape you create with the applet.

    When calculating or counting surface area of your shape, come up with a system to avoid omitting or double-counting faces.

  • See Possible Answers

    Two figures: a rectangular prism 4 by 2 by 1, and a 3 by 3 square with a hole measuring 1 cubic unit in the middle, labeled 'square donut'.

    Rectangular prism:

    The volume of the rectangular prism is 4 × 2 × 1 = 8 cubic units. This is the same result as counting the number of cubes used to build the prism.

    In the rectangular prism, face A has an area of 4 × 2 = 8 square units. Face B has an area of 2 square units. Face C has an area of 4 square units.
    Faces A, B, and C all have congruent opposing faces.
    The surface area of the rectangular prism, including the bottom, is therefore 2(8) + 2(2) + 2(4) = 28 square units.

    Square donut:

    The volume of the square donut, from counting the number of cubes it occupies, is 8 cubic units.

    In the rectangular prism, face D and E have the same area of 3 square units each.
    Face F has an area of 8 square units.
    Faces D, E, and F all have congruent opposing faces.
    There are 4 faces in the donut hole, which have a total area of 4 square units.
    The surface area of the square donut is therefore 4(3) + 2(8) + 4 = 32 square units.

    The volumes of both shapes are the same, because volume measures the number of unit cubes that can be packed into a figure. Both shapes are built using the same number of cubes. Building shapes with different volumes would mean using fewer or more cubes.

    Shapes with the same volume like these two can have different surface areas. Shapes with larger surface areas are more spread out and have more faces exposed. Shapes with smaller surface areas are more compact and have more of their faces hidden or shared with other cubes.




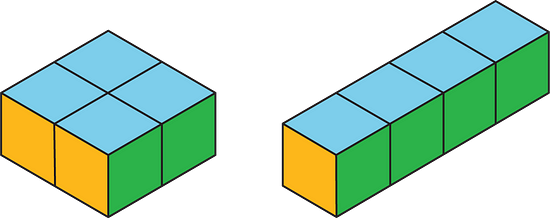
16.3 - Comparing Prisms Without Building Them

Three rectangular prisms each have a height of 1 cm.

Prism A has a base that is 1 cm by 11 cm.
Prism B has a base that is 2 cm by 7 cm.
Prism C has a base that is 3 cm by 5 cm.

1. Find the surface area and volume of each prism. Use the dot paper to draw the prisms, if needed.

2. Analyze the volumes and surface areas of the prisms. What do you notice? Write 1–2 observations about them.

  • Answers

    A field of dots, on which three rectangular prisms have been drawn. Prism A is 11 by 1 by 1 cm. Prism B is 2 by 7 by 1 cm. Prism C is 3 by 5 by 1 cm.

    1. A: Volume = 11 cubic cm
    Surface area = 4(11) + 2(1) = 46 sq cm
    B: Volume = 2 × 7 × 1 = 14 cubic cm
    Surface area = 2(2 × 7) + 2(7) + 2(2) = 46 sq cm
    C: Volume = 3 × 5 × 1 = 15 cubic cm
    Surface area = 2(3 × 5) + 2(5) + 2(3) = 46 sq cm

    2. The volumes of the prisms are all different, but the surface areas are the same.
    Shapes with different volumes can have the same surface area.
    Volume is described in terms of unit cubes and surface area in terms of the exposed faces of those unit cubes.


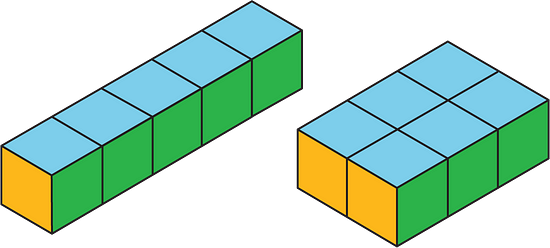
Can you find more examples of prisms that have the same surface areas but different volumes? How many can you find?

  • See Possible Answers

    These are 3 examples of prisms that all have a surface area of 54 sq cm, but different volumes. These are not necessarily the only prisms which can be drawn for a surface area of 54 sq cm.

    A field of dots, on which three rectangular prisms have been drawn. Prism A is 3 by 3 by 3 cm. Prism B is 3 by 6 by 1 cm. Prism C is 13 by 1 by 1 cm.

    1. A: Volume = 3 × 3 × 3 = 27 cubic cm
    Surface area = 6(3 × 3) = 54 sq cm
    B: Volume = 3 × 6 × 1 = 18 cubic cm
    Surface area = 2(3 × 6) + 2(6) + 2(3) = 54 sq cm
    C: Volume = 13 × 1 × 1 = 13 cubic cm
    Surface area = 4(13) + 2(1) = 54 sq cm


Lesson 16 Summary

Length is a one-dimensional attribute of a geometric figure. We measure lengths using units like millimeters, centimeters, meters, kilometers, inches, feet, yards, and miles.

Area is a two-dimensional attribute. We measure area in square units. For example, a square that is 1 centimeter on each side has an area of 1 square centimeter.

Volume is a three-dimensional attribute. We measure volume in cubic units. For example, a cube that is 1 kilometer on each side has a volume of 1 cubic kilometer.

Surface area and volume are different attributes of three-dimensional figures. Surface area is a two-dimensional measure, while volume is a three-dimensional measure.

Two figures can have the same volume but different surface areas. For example:

A rectangular prism with side lengths of 1 cm, 2 cm, and 2 cm has a volume of 4 cu cm and a surface area of 16 sq cm.
A rectangular prism with side lengths of 1 cm, 1 cm, and 4 cm has the same volume but a surface area of 18 sq cm.

Similarly, two figures can have the same surface area but different volumes.

A rectangular prism with side lengths of 1 cm, 1 cm, and 5 cm has a surface area of 22 sq cm and a volume of 5 cu cm.
A rectangular prism with side lengths of 1 cm, 2 cm, and 3 cm has the same surface area but a volume of 6 cu cm.

Practice Problems

1. Match each quantity with an appropriate unit of measurement.

  1. The surface area of a tissue box
  2. The amount of soil in a planter box
  3. The area of a parking lot
  4. The length of a soccer field
  5. The volume of a fish tank
  1. Square meters
  2. Yards
  3. Cubic inches
  4. Cubic feet
  5. Square centimeters
  • Answers
    1. The surface area of a tissue box: Square centimeters
    2. The amount of soil in a planter box: Cubic inches
    3. The area of a parking lot: Square meters
    4. The length of a soccer field: Yards
    5. The volume of a fish tank: Cubic inches

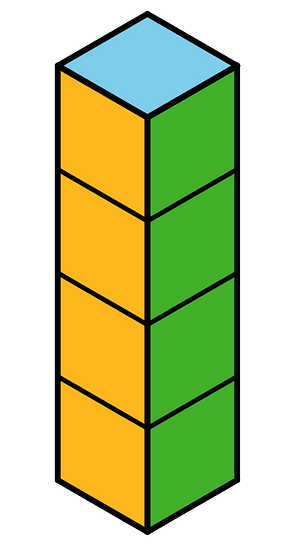
2. Here is a figure built from snap cubes.

a. Find the volume of the figure in cubic units.
b. Find the surface area of the figure in square units.
c. True or false: If we double the number of cubes being stacked, both the volume and surface area will double. Explain or show how you know.

  • Answers

    a. Volume of the figure = 1 unit × 1 unit × 4 units = 4 cubic units
    b. Surface area of the figure = 4(4 units) + 2(1 unit) = 18 square units
    c. False. The volume will double to 8 cubic units, but the new surface area will be 4(8 units) + 2(1 unit) = 34 square units, which does not equal 18 × 2.

3. Lin said, "Two figures with the same volume also have the same surface area."

a. Which two figures suggest that her statement is true?
b. Which two figures could show that her statement is not true?

  • Answers

    A: Volume = 6 cubic units, surface area = 26 square units
    B: Volume = 6 cubic units, surface area = 24 square units
    C: Volume = 6 cubic units, surface area = 24 square units
    D: Volume = 7 cubic units, surface area = 26 square units
    E: Volume = 5 cubic units, surface area = 22 square units

    B and C have the same volume and same surface area.
    A and C have the same volume, but a different surface area, showing that Lin's statement is not true.


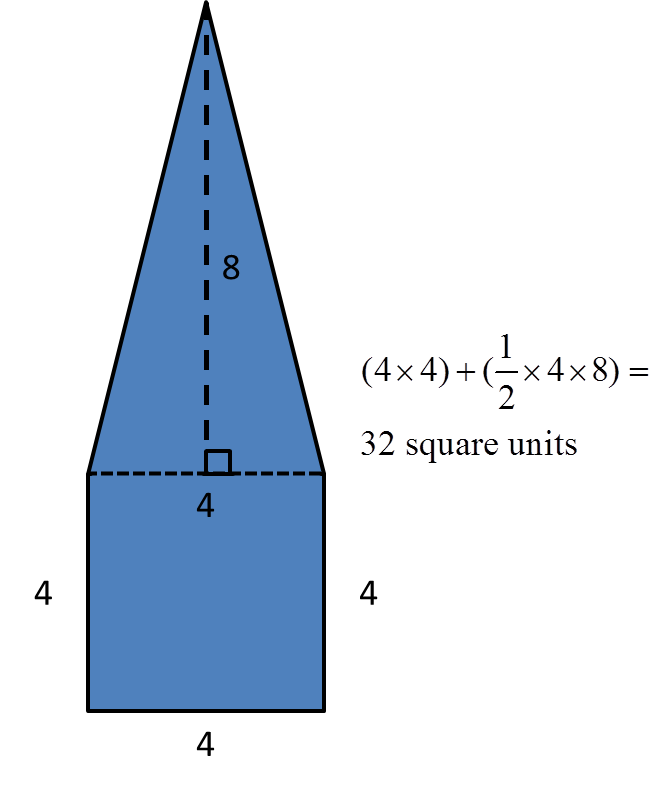
4. Draw a pentagon (five-sided polygon) that has an area of 32 square units. Label all relevant sides or segments with their measurements, and show that the area is 32 square units.

  • Hints

    This polygon does not need to be a regular pentagon, as long as it has 5 sides. Try a composite of a square and a triangle, and try different areas for the square. The triangle should have the same base length as the square's sides.

    Other compositions are possible.

  • Answers

    A five-sided polygon, composed of a square 4 by 4 attached to a triangle with base 4 and height 8.


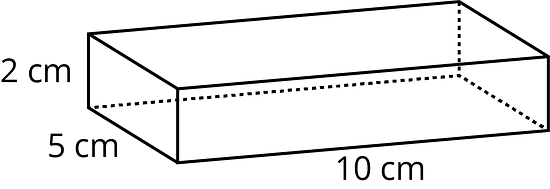
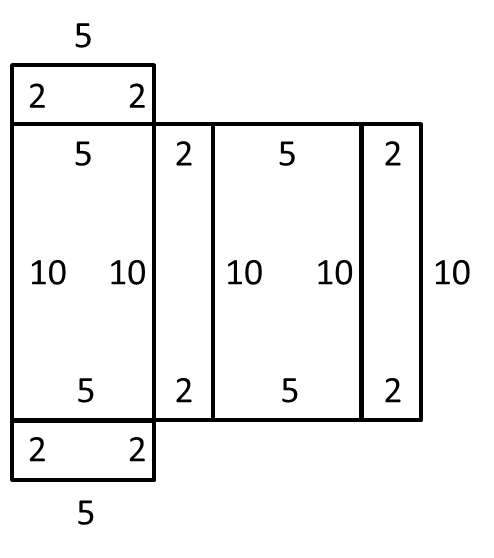
5. a. Draw a net for this rectangular prism.
b. Find the surface area of the rectangular prism.

  • Answers

    a.
    A net of a rectangular prism, consisting of 4 rectangles in a row with 1 rectangle above and 1 rectangle below the first rectangle. The first and third rectangles are 5 by 10, the second and fourth 2 by 10, and the rectangles above and below the first rectangle are both 5 by 2.

    b. The surface area is 2(5 × 10) + 2(2 × 10) + 2(2 × 5) = 160 sq cm.



The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
Mathway Calculator Widget


OML Search


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.



 
Back to Top | Interactive Zone | Home

Copyright © 2005, 2024 - OnlineMathLearning.com.
Embedded content, if any, are copyrights of their respective owners.