OML Search

Illustrative Mathematics Unit 6.1, Lesson 12: What is Surface Area?

Related Topics:
Math Worksheets




Learn about what it means to find the surface area of a three-dimensional object. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons


What is Surface Area?
Let’s cover the surfaces of some three-dimensional objects.

Illustrative Math Unit 6.1, Lesson 12 (printable worksheets)

12.1 - Covering the Cabinet (Part 1)

Watch the video to see a cabinet being partially tiled with numbered sticky notes (audio not necessary), or look at the photos:

4 photographs of a teacher covering the outside of a large cabinet with sticky notes. The last photograph shows the back of the cabinet partially covered with notes numbered 1-48.

Estimate an answer to the question: How many sticky notes would it take to cover the cabinet, excluding the bottom?





12.2 - Covering the Cabinet (Part 2)

Earlier, you learned about a cabinet being covered with sticky notes.

1. How could you find the actual number of sticky notes it will take to cover the cabinet, excluding the bottom? What information would you need to know?

2. Use the information you have to find the number of sticky notes to cover the cabinet. Show your reasoning.

  • Possible Answers to Question 1 and Required Information

    1. You would need to know the area of each face of the cabinet, excluding the bottom, in terms of sticky notes. To do this you would need to know the dimensions of the cabinet.

    The cabinet is 24 (height) by 12 (width) by 6 (depth) sticky notes.

    Note that only opposite sides of the cabinet can be presumed to be congruent, and that you do not need to cover the bottom of the cabinet. For the purpose of this exercise, you do not need to account for the door handles.

  • Answer to Question 2

    2. The back face of the cabinet requires 24 × 12 = 288 sticky notes. The back and front faces together require 288 × 2 = 576 sticky notes.
    One side of the cabinet requires 6 × 24 = 144 sticky notes. The two sides together require 2 × 144 = 288 sticky notes.
    The top requires 12 × 6 = 72 sticky notes.
    Covering all faces of the cabinet, excluding the bottom, will take 576 + 288 + 72 = 936 sticky notes.

    You may watch the video demonstrating this here under "Act 3". Note that this video uses 935 sticky notes, because the video shows a real cabinet with door handles.

  • What is Surface Area?

    The surface area of a three-dimensional figure is the total area of all its faces.
    A face is a single flat surface on a three-dimensional figure.

    In this exercise you calculated the surface area of a cabinet, excluding the bottom, in units of sticky notes. The units can change. If we used larger sticky notes, we would need fewer notes to cover the surface area of the same cabinet. If we used smaller ones, we would need more.


How many sticky notes are needed to cover the outside of 2 cabinets pushed together side by side (including the bottom)? What about 3 cabinets? 20 cabinets?

  • Hints

    Use the previous calculations to work out how many sticky notes are required to cover 1 cabinet including its bottom.

    If 2 cabinets are pushed together side by side and considered as a single object, 2 side faces (1 from each) are no longer on the outside, and should not be included when calculating the surface area.
    If 3 cabinets are pushed together, 4 side faces are hidden.
    If 4 cabinets are pushed together, 6 side faces are hidden. Note the pattern in the number of hidden side faces.
    If 20 cabinets are pushed together, 38 side faces are hidden.

  • Answers

    From our previous calculations:
    Area of back or front of cabinet = 288 sticky notes
    Area of 1 side = 144 sticky notes
    Area of top = 72 sticky notes
    Surface area of cabinet excluding bottom = 936 sticky notes
    The bottom of the cabinet will be congruent with its top. Hence, covering a cabinet including its bottom will require 936 + 72 = 1008 sticky notes.

    2 separate cabinets will have a total surface area of 2 × 1008 = 2016 sticky notes.
    If the 2 cabinets are pushed together side by side and considered as a single object, 2 side faces (1 from each) are no longer on the outside. The surface area of the 2 cabinets pushed together is then 2016 - (2 × 144) = 1728 sticky notes.

    For 3 cabinets pushed together, 4 side faces are hidden. The surface area is (3 × 1008) - (4 × 144) = 2448 sticky notes.

    For 20 cabinets pushed together, 38 side faces are hidden. The surface area is (20 × 1008) - (38 × 144) = 14688 sticky notes.




12.3 - Building with Snap Cubes

Here is a rectangular prism built from 12 cubes:

It has six faces, but you can only see three of them in the sketch. It has a surface area of 32 square units.

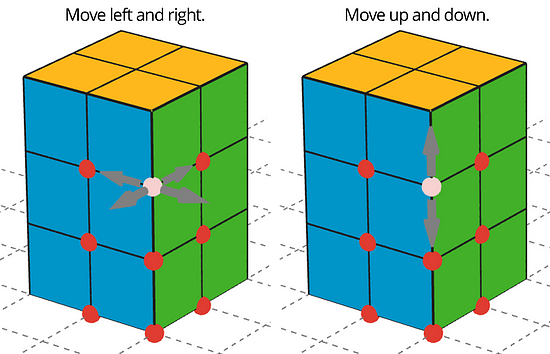
Open the applet. Drag the red point on the block on the gray square to move it. Click on the red points to change from left/right movement to up/down movement, as illustrated below.

The gray square will give you 12 blocks in total. Use all 12 cubes in the applet to build a different rectangular prism (with different edge lengths than shown in the prism here). You can turn the view to see all of the faces of your figure.

1. How many faces does your figure have?

2. What is the surface area of your figure in square units?

  • See Possible Answers

    A rectangular prism built from 12 cubes, 6 by 2 by 1.

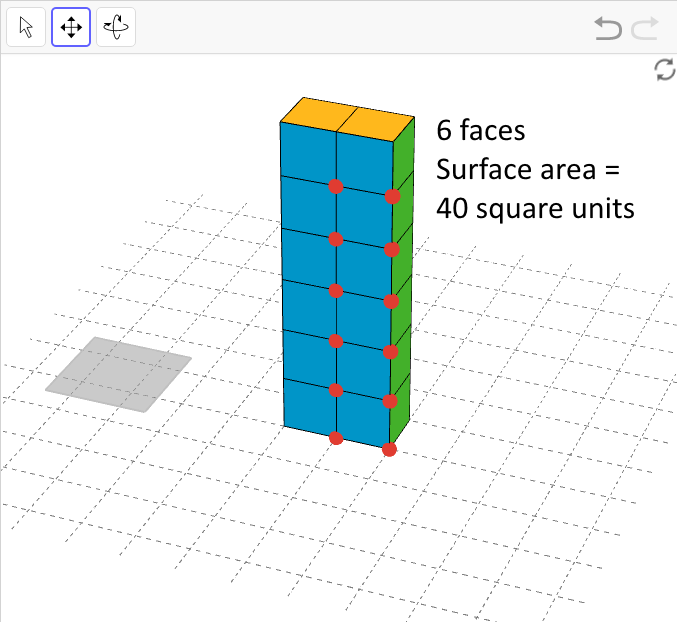
    This rectangular prism is composed of 12 cubes like the first prism in the question, but is 6 (height) by 2 (width) by 1 (depth) instead.

    1. This figure has 6 faces, of which 3 are visible from this angle.

    2. To find the surface area, find the area of each face and add them up.
    In this image, the blue face has an area of 6 × 2 = 12 square units.
    The yellow face has an area of 1 × 2 = 2 square units.
    The green face has an area of 6 × 1 = 6 square units.
    In a rectangular prism, the opposing faces are congruent to each other, so we can multiply the above measurements by 2 to get the area of each pair of faces.
    Hence, the surface area of the prism is 2 × 12 + 2 × 2 + 2 × 6 = 40 square units.


Lesson 12 Summary

The surface area of a figure (in square units) is the number of unit squares it takes to cover the entire surface of an object without gaps or overlaps.
If a three-dimensional figure has flat sides, the sides are called faces.
The surface area is the total of the areas of the faces.

For example, a rectangular prism has six faces. The surface area of the prism is the total of the areas of the six rectangular faces.

So the surface area of a rectangular prism that has edge-lengths 2 cm, 3 cm, and 4 cm has a surface area of (2 × 3) + (2 × 3) + (2 × 4) + (2 × 4) + (3 × 4) + (3 × 4) = 52 square centimeters.



Glossary Terms

face

Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.

surface area

The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.

For example, if the faces of a cube each have an area of 9 cm2, then the surface area of the cube is 6 × 9, or 54 cm2.



Practice Problems

1. What is the surface area of this rectangular prism?

A: 16 square units
B: 32 square units
C: 48 square units
D: 64 square units

  • Answers

    The surface area of this prism is 2(4 × 4) + 2(2 × 4) + 2(2 × 4) = 64 square units.
    The answer is D: 64 square units.


2. Which description can represent the surface area of this trunk?

A: The number of square inches that cover the top of the trunk.
B: The number of square feet that cover all the outside faces of the trunk.
C: The number of square inches of horizontal surface inside the trunk.
D: The number of cubic feet that can be packed inside the trunk.

  • Answers

    B: The number of square feet that cover all the outside faces of the trunk.
    The definition of surface area is the number of unit squares it takes to cover the entire surface, or all the outside faces, of an object without gaps or overlaps.


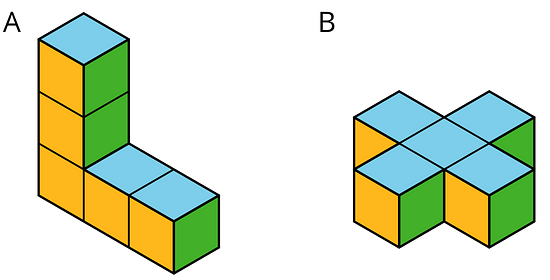
3. Which figure has a greater surface area?

  • Answers

    Figure A has 8 faces. The total area of these is 2(5) + 3 + 3 + 1 + 2 + 2 + 1 = 22 square units.

    Figure B has 14 faces. The total area of these is 2(5) + 12(1) = 22 square units.

    Both figures have the same surface area.


4. A rectangular prism is 4 units high, 2 units wide, and 6 units long. What is its surface area in square units? Explain or show your reasoning.

  • Answers

    The surface area of this rectangular prism is 2(4 × 2) + 2(2 × 6) + 2(4 × 6) = 88 square units.


5. Draw an example of each of these triangles on the grid.

A. A right triangle with an area of 6 square units.
B. An acute triangle with an area of 6 square units.
C. An obtuse triangle with an area of 6 square units.

  • See Possible Answers

    Three triangles drawn on a grid that is 16 units by 10 units. Triangle A is a right triangle with a base of 4 units and a height of 3 units. Triangle B is an acute triangle with a base of 3 units and a height of 4 units. Triangle C is an obtuse triangle with a base of 2 units and a height of 6 units.

    A: ½ × 4 units × 3 units = 6 sq units
    B: ½ × 3 units × 4 units = 6 sq units
    C: ½ × 2 units × 6 units = 6 sq units


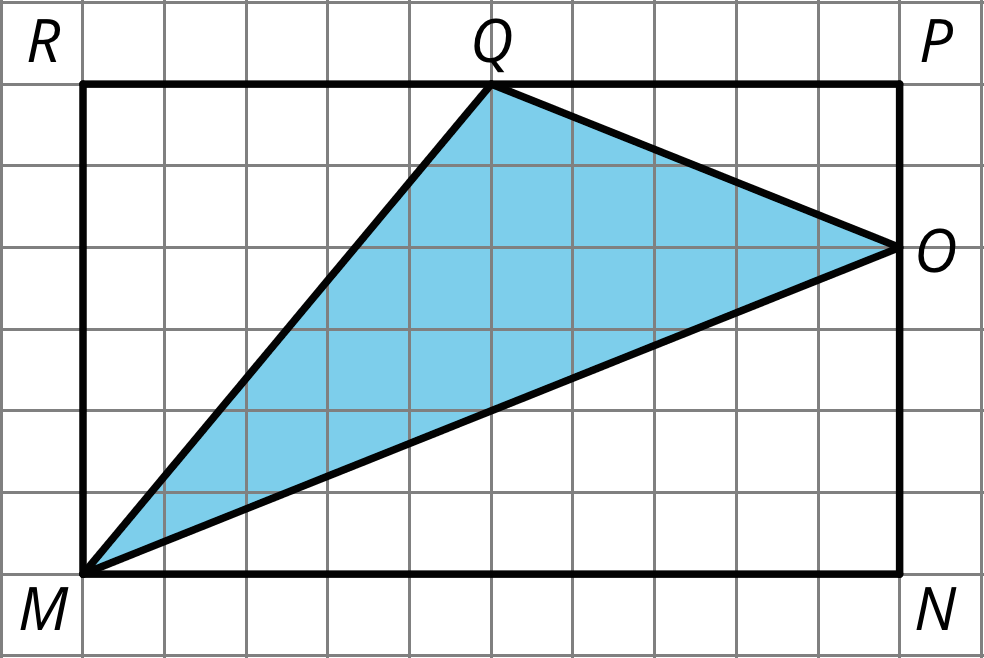
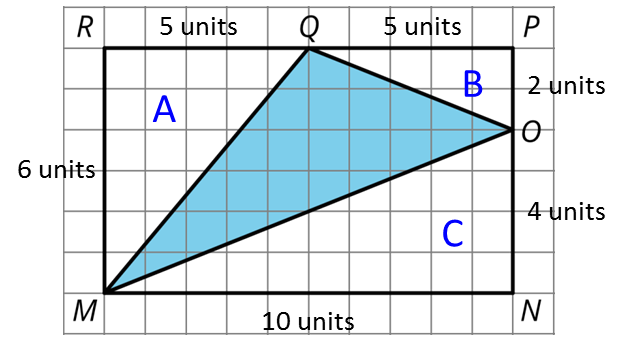
6. Find the area of triangle MOQ in square units. Show your reasoning.

  • Answers

    A triangle with vertices labeled M, Q, and P. Triangle MQP is enclosed in a rectangle MRPN. Sides MR and PN of the rectangle are six units high, and sides RP and MN of the rectangle are 10 units long. Vertex Q is five units across side RP, and vertex O is 2 units down on side PN. The unshaded triangles formed by the enclosing rectangle have been labeled A, B, and C. A has base 5 units and height 6 units. B has base 5 units and height 2 units. C has base 10 units and height 4 units.

    The area of rectangle MRPN is 6 units × 10 units = 60 square units.
    Triangle A: ½ × 5 units × 6 units = 15 square units.
    Triangle B: ½ × 5 units × 2 units = 5 square units.
    Triangle C: ½ × 10 units × 4 units = 20 square units.
    The area of the shaded region is 60 - (15 + 5 + 20) = 20 square units.


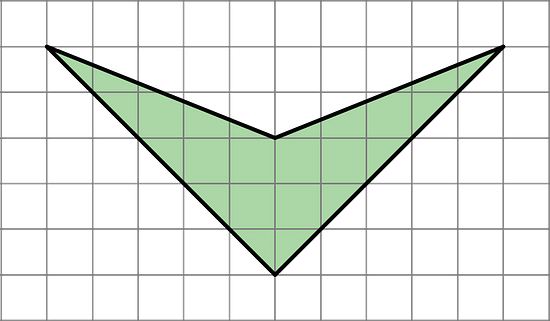
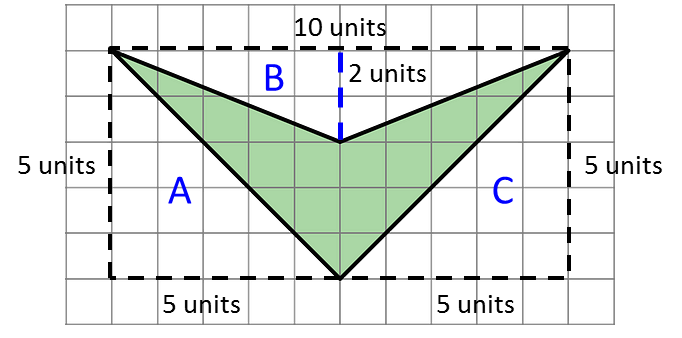
7. Find the area of this shape. Show your reasoning.

  • Answers

    A four-sided shape on a grid, with two sides that drop 5 units as they cross 5 units and meet at a right angle, and two sides that drop two units as they cross 5 units. The shape has been enclosed in a rectangle 5 by 10 units, creating 3 unshaded triangles labeled A, B, and C. A and C have base 5 units and height 5 units. B has base 10 units and height 2 units.

    The area of the enclosing rectangle is 10 units × 5 units = 50 square units.
    Triangle A: ½ × 5 units × 5 units = 12.5 square units.
    Triangle B: ½ × 10 units × 2 units = 10 square units.
    Triangle C: ½ × 5 units × 5 units = 12.5 square units.
    The area of the shaded region is 50 - (12.5 + 10 + 12.5) = 15 square units.




The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
Mathway Calculator Widget


OML Search


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.



 
Back to Top | Interactive Zone | Home

Copyright © 2005, 2024 - OnlineMathLearning.com.
Embedded content, if any, are copyrights of their respective owners.