Sum And Difference Identities

What are the Sum and Difference Identities?

Sum and difference identities are a set of trigonometric formulas that allow you to express trigonometric functions of the sum or difference of two angles in terms of trigonometric functions of those individual angles. These identities are useful for simplifying expressions, solving equations, and finding exact values of trigonometric functions.

The following diagram shows the Sum and Difference Identities for sin, cos and tan. Scroll down the page for more examples and solutions on how to use the identities.

 

How to Remember the Sum and Difference Identities? (Mnemonics & Patterns)
It is often necessary to memorize these identities for quick application. Here are some common ways to remember them:

Sine (Same Sign): “Sin-Cos, Cos-Sin, and the sign’s the same."
\(sin(A \pm B) = sin(A)cos(B) \pm cos(B)sin(A)\)

Cosine (Opposite Sign): “Cos-Cos, Sin-Sin, and the sign is opposite."
\(cos(A \pm B) = cos(A)cos(B) \mp sin(A)sin(B)\)

Tangent: Think of the numerator as having the “sum/difference” behavior of the original angles, and the denominator as “1 opposite product."
\(tan(A + B) = \frac{tan(A) + tan(B)}{1 - tan(A)tan(B)}\)
\(tan(A - B) = \frac{tan(A) - tan(B)}{1 + tan(A)tan(B)}\)

Example:

Solution:
Given that cos(α + β) = cos α cos β – sin α sin β, then

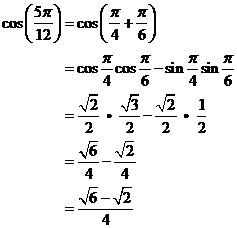
Example:

Solution:

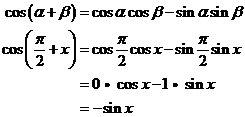
How to use the sum and difference identities for sin, cos, and tan?
Example:

1. Find sin(105°) exactly
2. Find cos(105°) exactly
3. Find tan(105°) exactly

• Show Video Lesson

How to use Sum and Difference Identities to find exact trig values?
Example:

1. Find \(\cos \left( {\frac{{3\pi }}{4},\frac{\pi }{3}} \right)\) exactly
2. Find cos(42°)cos(18°) - sin(42°)sin(18°) exactly
3. Find \(\frac{{\tan 80^\circ - \tan 35^\circ }}{{1 + \tan 80^\circ \tan 35^\circ }}\) exactly
4. Find cos(u + v) exactly if sin(u) = 3/5 and sin(v) = 12/13 where u and v are acute angles (quadrant I)

• Show Video Lesson

How to use the Sum and Difference Identities to Prove Other Identities
Example:
Prove sin(α + β) - sin(α - β) = 2cosαsinβ

• Show Video Lesson

Using the Sum and Difference Identities for Sine, Cosine and Tangent
Example 1:
If sin x = 12/13 and x is in the first quadrant, find tan(2x)

• Show Video Lesson

Using the Sum and Difference Identities for Sine, Cosine and Tangent
Example 2:
If tan x = 5/3 and x is in the first quadrant, find sin(2x)

• Show Video Lesson

Using the Sum and Difference Identities for Sine, Cosine and Tangent
Example 3:
Simplify 1 - 16sin²x cos²x

• Show Video Lesson

Key Applications

1. Finding Exact Values:
   These identities can be used to find the exact values of trigonometric functions for angles that are not directly on the unit circle. For example, you can find sin(75°) by expressing it as sin(45° + 30°).
2. Simplifying Expressions:
   They can help simplify complex trigonometric expressions, making them easier to work with.
3. Solving Trigonometric Equations:
   These identities are essential tools for solving various trigonometric equations.

Important Notes:

• It’s crucial to remember the signs in these formulas, as they can easily lead to errors.
• These identities are valid for any angles A and B.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.