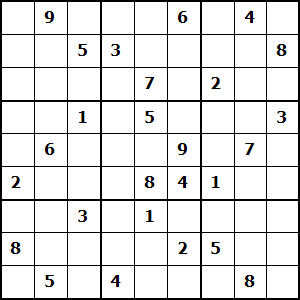
Sudoku Rules
How to play Sudoku?
Try to fill the grid with the integers 1 to 9 such that each row, column, and box (3×3 regions bordered by thick lines) contains a single instance of all the integers from 1 to 9.
Take a look at the following example. Click on the image to see the solution. You would notice that each row has an instance of 1 to 9, each column has an instance of 1 to 9 and each 3 × 3 box has an instance of 1 to 9. A well designed sudoku puzzle would have only one possible solution.
Although the sudoku rules are simple, the difficulty of a sudoku puzzle may range from very easy to very hard. This could have contributed to the popularity of sudoku as it can be designed as a puzzle for kids or a puzzle for the experts.
There are also many variations of sudoku that can make the puzzle even more challenging than the basic 9 × 9 puzzle.
Learn How To Solve Sudoku
Solving Sudoku involves several different logical methods or strategies.
Have a look at this video series of Sudoku Tips which will show you the different techniques that can be used to solve Sudoku Puzzles.
Here’s an e-book that teaches the methods of solving Sudoku and has lots of Sudoku puzzles that you can practice with - Sudoku By Steps
Sudoku Puzzles
You may want to try out the following Sudoku puzzles.
Sudoku - with different levels of difficulty from "2x2 trivial" to to "3x3 killer"
Sudoku from easiest to hardest - Test your skills with the different levels of Sudoku.
Also check out this page for more Sudoku puzzles.
History Of Sudoku
The puzzle seems to have first been published in New York in the late 1970s by the specialist puzzle publisher Dell in its magazine Math Puzzles and Logic Problems, under the title Number Place. The person who designed the puzzle and composed the first of its kind is not recorded, but it was probably Walter Mackey, one of Dell’s puzzle constructors.
The puzzle was introduced in Japan by Nikoli in the paper Monthly Nikolist in April 1984 as “Sūji wa dokushin ni kagiru (数字は独身に限る)”, which can be translated as “the numbers must be single” or “the numbers must occur only once” (独身 literally means “single; celibate; unmarried”). The puzzle was named by Kaji Maki (鍜治 真起), the president of Nikoli. At a later date, the name was abbreviated to Sudoku (数独, pronounced sue-do-koo; sū = number, doku = single); it is a common practice in Japanese to take only the first kanji of compound words to form a shorter version. In 1986, Nikoli introduced two innovations which guaranteed the popularity of the puzzle: the number of givens was restricted to no more than 30 and puzzles became “symmetrical” (meaning the givens were distributed in rotationally symmetric cells). It is now published in mainstream Japanese periodicals, such as the Asahi Shimbun. Nikoli still holds the trademark for the name Sudoku; other publications (at least in Japan) use other names.
In 1997, retired Hong Kong judge Wayne Gould, 59, a New Zealander, was enticed by seeing a partly completed puzzle in a Japanese bookshop. He went on to develop a computer program that spontaneously produces puzzles; this took over six years. He promoted the puzzle to The Times in Britain, which launched it on 12 November 2004. Three days later The Daily Mail began to publish the puzzle under the name “Codenumber”. Nationwide News Pty Ltd began publishing the puzzle in The Daily Telegraph on 20th May 2005; five puzzles with solutions were printed that day. The puzzles by Pappocom, Wayne Gould’s software house, have been printed daily ever since. The immense popularity of Sudoku in British newspapers and internationally has led to it being dubbed in the world media in 2005 variously as “the Rubik’s cube of the 21st century” or the “fastest growing puzzle in the world”.
Bringing the process full-circle, Kappa reprints Nikoli Sudoku in GAMES Magazine under the name Squared Away; the New York Post is now also publishing the puzzle. It is also often included in puzzle anthologies, such as The Giant 1001 Puzzle Book (under the title Nine Numbers).
Curiously, Dell, the apparent inventors of the puzzle, have made no attempts to cash in on this phenomenon, or even release a public statement about it.
Mathematical Trivia
The general problem of solving Sudoku puzzles on n2×n2 boards of n×n blocks is known to be NP-complete. This gives some vague indication of why Sudoku is hard to play, but on ordinary 9 × 9 or 16 × 16 boards the problem is finite and can be solved by a deterministic finite automaton that knows the entire game tree. However, for a non-trivial starting board, the game tree is very large and so this method is not feasible. The problem of solving a puzzle that is known to have only one solution is in UP.
Solving Sudoku puzzles can be expressed as a graph coloring problem. The aim of the puzzle in its standard
form is to construct a proper 9-coloring of a particular graph, given a partial 9-coloring. The graph in
question has 81 vertices, one vertex for each cell of the grid. The vertices can be labeled with the ordered
pairs 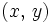 , where x and y are integers between 1 and 9. In this case, two
distinct vertices labeled by
, where x and y are integers between 1 and 9. In this case, two
distinct vertices labeled by 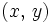 and
and 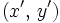 are joined by an edge if and only if:
are joined by an edge if and only if:
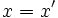 , or,
, or,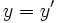 , or,
, or,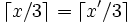 and
and 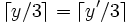
The puzzle is then completed by assigning an integer between 1 and 9 to each vertex, in such a way that vertices that are joined by an edge do not have the same integer assigned to them.
A valid Sudoku solution grid is also a Latin square. There are significantly fewer valid Sudoku solution grids than Latin squares because Sudoku imposes the additional regional constraint. Nonetheless, the number of valid Sudoku solution grids for the standard 9×9 grid was calculated by Bertram Felgenhauer in 2005 to be 6,670,903,752,021,072,936,960, which is roughly the number of micrometers to the nearest star. The result was derived through logic and brute force computation. The derivation of this result was considerably simplified by analysis provided by Frazer Jarvis and the figure has been confirmed independently by Ed Russell. The number of valid Sudoku solution grids for the 16×16 derivation is not known.
The maximum number of givens that can be provided while still not rendering the solution unique, regardless of variation, is four short of a full grid; if two instances of two numbers each are missing and the cells they are to occupy are the corners of an orthogonal rectangle, there are two ways the numbers can be added. The inverse of this - the fewest givens that render a solution unique - is an unsolved problem, although the lowest number yet found for the standard variation without a symmetry constraint is 17, a number of which have been found by Japanese puzzle enthusiasts, and 18 with the givens in rotationally symmetric cells.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.