Illustrative Mathematics Unit 6.1, Lesson 17: Squares and Cubes

Related Topics:
Math Worksheets

Learn more about squares, cubes, and how exponents relate to the area or volume of squares and cubes. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons

Squares and Cubes
Let’s investigate perfect squares and perfect cubes.

Illustrative Math Unit 6.1, Lesson 17 (printable worksheets)

17.1 - Perfect Squares

1. The number 9 is a perfect square.
Find four numbers that are perfect squares and two numbers that are not perfect squares.

2. A square has side length 7 km. What is its area?

3. The area of a square is 64 sq cm. What is its side length?

• Hints

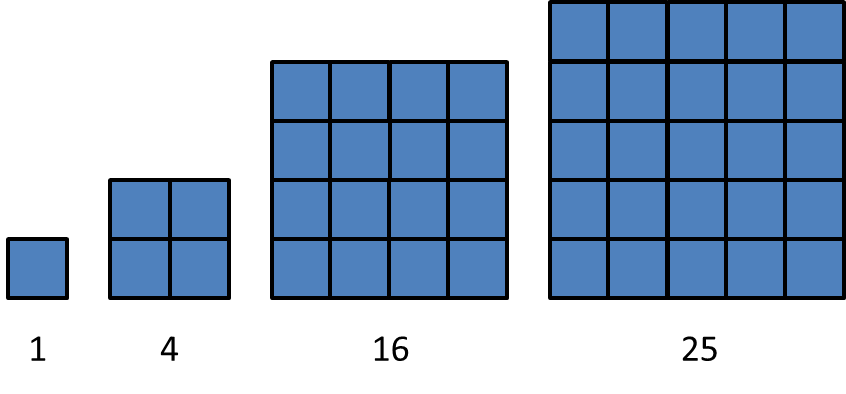
  1. A number is a perfect square when that number of small squares can be arranged into a large square. For example, 9 is a perfect square because 9 copies of a small square can be arranged into a large square:
  

  However, 10 is not a perfect square because 10 copies of a small square cannot be arranged into a large square:
  

  3. To find the side length, you need to find a number which, when multiplied by itself, equals 64. Answer questions 1 and 2 first. Do you get answers more or less than 64? What does that tell you about the number you need?

• Answers

  1. Perfect squares: 1, 4, 16, 25
  Non-perfect squares: 5, 24
  A number is a perfect square when that number of small squares can be arranged into a large square:
  

  2. 7 km × 7 km = 49 sq km

  3. 8 cm × 8 cm = 64 sq cm

• See Video 1 for Whole Lesson
• See Video 2 for Whole Lesson

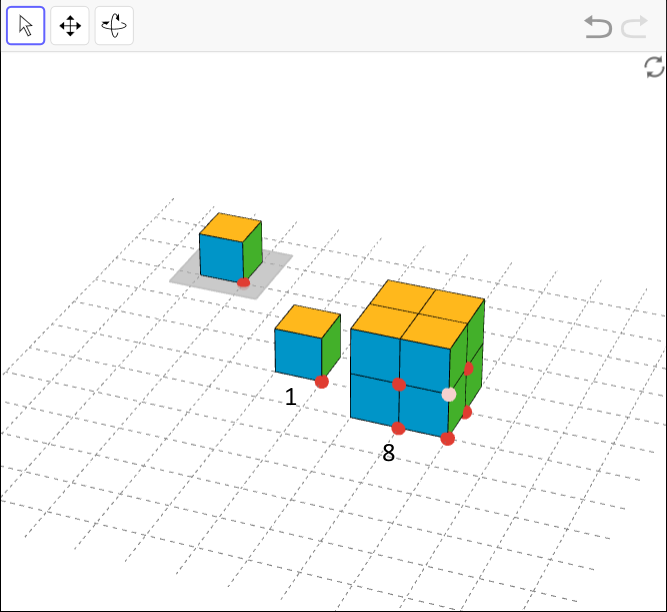
17.2 - Building with 32 Cubes

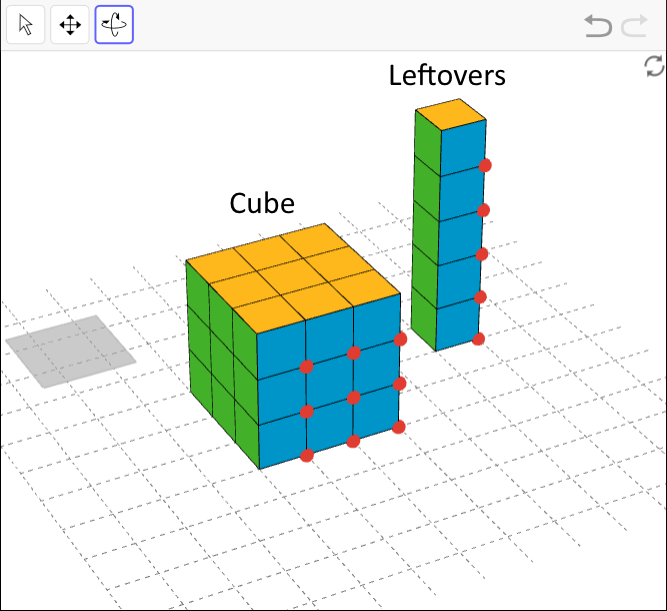
Open the applet. Drag on the red point on the cube to move it, and click on the point to switch between vertical and horizontal movement. The gray square will give you 32 cubes. Use as many of these as you need to build the largest single cube you can. Each small cube has a side length of 1 unit.

1. How many snap cubes did you use?
2. What is the side length of the cube you built?
3. What is the area of each face of the built cube? Show your reasoning.
4. What is the volume of the built cube? Show your reasoning.

• Hints

  32 is not a perfect cube. You do not need to use all of the cubes in the applet.

• See Possible Answers

  

  1. The built cube consists of 27 snap cubes. There are 5 leftover snap cubes.

  2. The built cube has a side length of 3.

  3. The area of any one face of the built cube is 3 × 3 = 9 sq units.

  4. The volume of the built cube is 3 × 3 × 3 = 27 cubic units. This is equal to the number of snap cubes used.

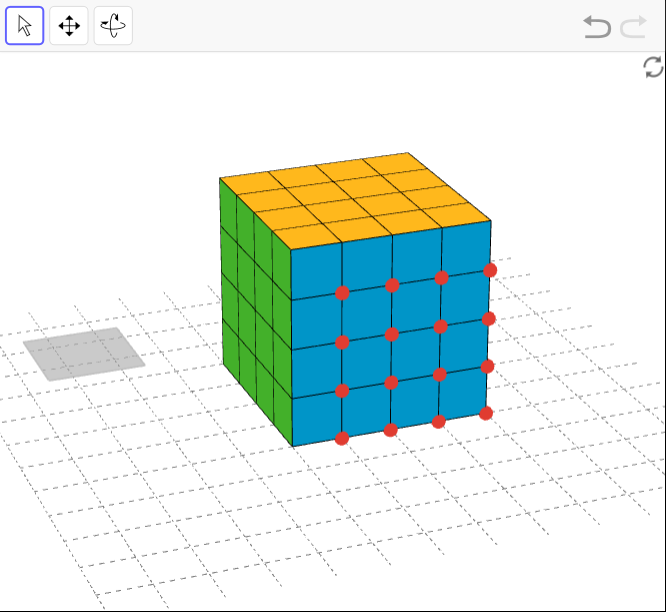
Open the next applet. The gray square will give you 64 cubes. (There is an error in the applet title.) Use as many cubes as you need to build the largest single cube you can.

1. How many snap cubes did you use?
2. What is the edge length of the new cube you built?
3. What is the area of each face of the built cube? Show your reasoning.
4. What is the volume of the built cube? Show your reasoning.

• Hints

  64 is a perfect cube.

• See Possible Answers

  

  1. The built cube consists of 64 snap cubes. 64 is a perfect cube, so there are no leftovers.

  2. The built cube has an edge length of 4.

  3. The area of any one face of the built cube is 4 × 4 = 16 sq units.

  4. The volume of the built cube is 4 × 4 × 4 = 64 cubic units. This is equal to the number of snap cubes used.

17.3 - Perfect Cubes

• Show Image
  

1. The number 27 is a perfect cube.
Find four other numbers that are perfect cubes and two numbers that are not perfect cubes.

2. A cube has side length 4 cm. What is its volume?

3. A cube has side length 10 inches. What is its volume?

4. A cube has side length s units. What is its volume?

• Hints

  Like perfect squares, a number is a perfect cube when that number of small cubes can be assembled into a larger cube.

  From the previous questions, a cube with a volume of 27 cubic units measures 3 × 3 × 3, and a cube with a volume of 64 cubic units measures 4 × 4 × 4. How might you find more numbers that are perfect cubes?

• Answers

  

  1. Perfect cubes: 1, 8, 64, 125
  Non-perfect cubes: 9, 16
  A number is a perfect cube when that number of small cubes can be assembled into a larger cube. Some examples are shown in the picture above.

  2. 4 cm × 4 cm × 4 cm = 64 cubic cm

  3. 10 in × 10 in × 10 in = 1000 cubic in

  4. s × s × s

17.4 - Introducing Exponents

When we multiply two of the same number together, such as 5 × 5, we say we are squaring the number. We can write the expression as 5². Because 5 × 5 is 25, we can write 5² = 25, and we say, "5 squared is 25". We can also say that 25 is a perfect square. The raised 2 in 5² is called an exponent.

When we multiply three of the same number together like 4 × 4 × 4, we say we are cubing the number. We can write it as 4³. Because 4 × 4 × 4 is 64, we can write 4³ = 64, and we say, "4 cubed is 64". We can also say that 64 is a perfect cube. The raised 3 in 4³ is also an exponent.

Exponents are also used as shorthand for units of area (square units) and units of volume (cubic units).
A square with side length 5 inches has area of 25 square inches, which we can write as 25 in².
A cube with edge length 4 centimeters has a volume of 64 cubic centimeters, which we can write as 64 cm³.

For these questions, make sure to include correct units of measure as part of each answer.

1. A square has side length 10 cm. Use an exponent to express its area.
2. The area of a square is 7² sq in. What is its side length?
3. The area of a square is 81 m². Use an exponent to express this area.
4. A cube has edge length 5 in. Use an exponent to express its volume.
5. The volume of a cube is 6³ cm³. What is its edge length?
6. A cube has edge length s units. Use an exponent to write an expression for its volume.

• Answers
  1. 10² cm² (which is equal to 100 cm²)
  2. 7 in
  3. 9² m²
  4. 5³ in³ (which is equal to 125 in³)
  5. 6 cm
  6. s³

The number 15,625 is both a perfect square and a perfect cube. It is a perfect square because it equals 125². It is also a perfect cube because it equals 25³. Find another number that is both a perfect square and a perfect cube. How many of these can you find?

• See Possible Answers

  1 equals both 1² and 1³.
  64 equals both 8² and 4³.

  There are an infinite number of possible answers.

Lesson 17 Summary

When we multiply two of the same numbers together, such as 5 × 5, we say we are squaring the number. We can write it like this: 5²

Because 5 × 5 is 25, we can write 5² = 25, and we say, "5 squared is 25".

When we multiply three of the same number together like 4 × 4 × 4, we say we are cubing the number. We can write it as 4³.

Because 4 × 4 × 4 is 64, we can write 4³ = 64, and we say, "4 cubed is 64".

We also use this notation for square and cubic units.
A square with side length 5 inches has area 25 in².
A cube with edge length 4 centimeters has a volume 64 cm³.

To read 25 in², we say "25 square inches", just like before.

The area of a square with side length 7 kilometers is 7² km². The volume of a cube with edge length 2 millimeters is 2³ mm³.

In general, the area of a square with side length s is s², and the volume of a cube with edge length s is s³.

Glossary Terms

cubed

We use the word cubed to mean "to the third power". This is because a cube with side length s has a volume of s × s × s, or s³.

---

exponent

In expressions like 5³ and 8², the 3 and the 2 are called exponents. They tell you how many factors to multiply. For example, 5³ = 5 × 5 × 5, and 8² = 8 × 8.

squared

We use the word squared to mean "to the second power". This is because a square with side length s has an area of s × s, or s².

Practice Problems

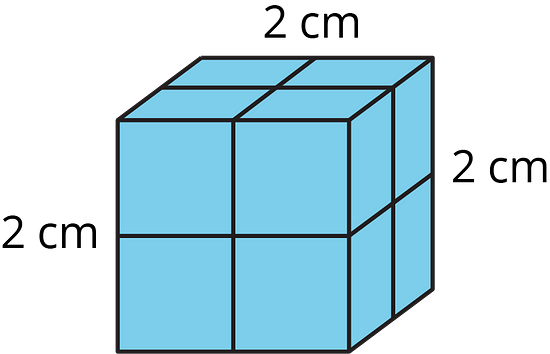
1. What is the volume of this cube?

• Show Image
  

• Answers

  2³ cm³ = 8 cm³

2. a. Decide if each number on the list is a perfect square.
b. Write a sentence that explains your reasoning.

1. 16
2. 20
3. 25
4. 100
5. 125
6. 144
7. 225
8. 10,000

• Hints

  Use your knowledge of times tables or multiplications of 10: if a number in the list is not the result of multiplying a number by itself, it is not a perfect square.

• Answers
  1. 16 = 4²
  2. 20 = 4 × 5 or 2 × 10, not a perfect square
  3. 25 = 5²
  4. 100 = 10²
  5. 125 is not a perfect square; the closest perfect square is 121 = 11²
  6. 144 = 12²
  7. 225 = 15²
  8. 10,000 = 100²

3. a. Decide if each number on the list is a perfect cube.
b. Explain what a perfect cube is.

1. 1
2. 3
3. 8
4. 9
5. 27
6. 64
7. 100
8. 125

• Answers
  1. 1 = 1³
  2. 3 is a prime number and is not a perfect cube.
  3. 8 = 2³
  4. 9 = 3², not a perfect cube
  5. 27 = 3³
  6. 64 = 4³
  7. 100 = 10², not a perfect cube
  8. 125 = 5³

  If a given number of cubes can be arranged into a larger cube, that number is a perfect cube. Another way of expressing this is that a perfect cube is the result of raising any whole number to the third power.

4. a. A square has side length 4 cm. What is its area?
b. The area of a square is 49 m². What is its side length?
c. A cube has edge length 3 in. What is its volume?

• Answers

  a. 4² cm² = 16 cm²

  b. 49 m² = 7² m²
  Side length = 7 m

  c. 3³ in³ = 27 in³

5. Prism A and Prism B are rectangular prisms. Prism A is 3 inches by 2 inches by 1 inch. Prism B is 1 inch by 1 inch by 6 inches.

Select all statements that are true about the two prisms.

A: They have the same volume.
B: They have the same number of faces.
C: More inch cubes can be packed into Prism A than into Prism B.
D: The two prisms have the same surface area.
E: The surface area of Prism B is greater than that of Prism A.

• Answers

  A: True. Both Prism A and Prism B have a volume of 6 cubic inches.

  B: True. Both are rectangular prisms, which must have 6 faces.

  C: False. Both Prism A and Prism B have the same volume, and therefore can hold the same number of inch cubes.

  D: False. Surface area of Prism A = 2(3 × 2) + 2(3 × 1) + 2(2 × 1) = 22 in².
  Surface area of Prism B = 4(6) + 2(1) = 26 in².

  E: True. As seen in the explanation of D above, Prism B has a greater surface area than Prism A.

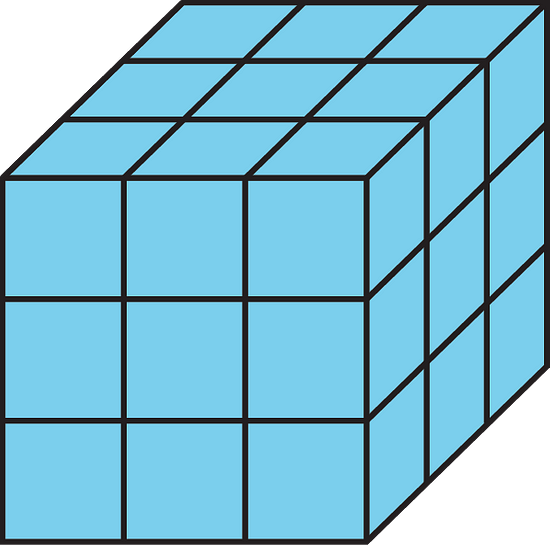
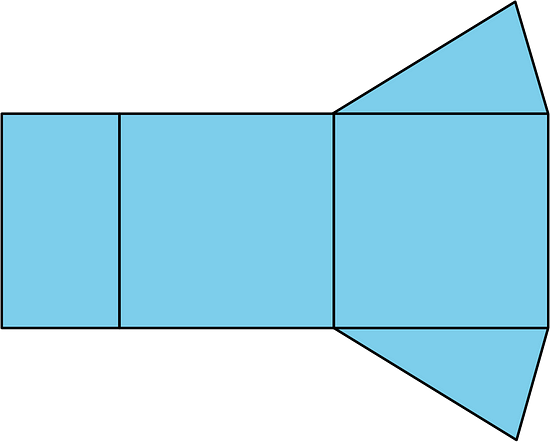
6. a. What polyhedron can be assembled from this net?

• Show Image
  

b. What information would you need to find its surface area? Be specific, and label the diagram as needed.

• See Possible Answers

  a. This net can be assembled into a triangular prism.

  b. The side lengths of the rectangles (s₁, s₂, s₃, and s₄), and the height of the triangles h is needed. s₁, s₂, and s₃ are also equal to the side lengths of the triangles.

  

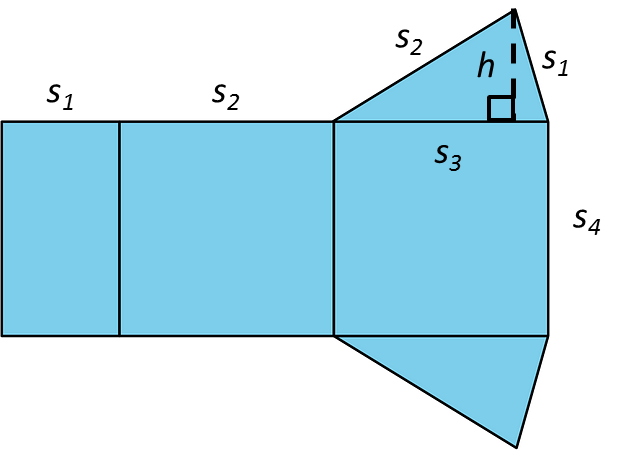
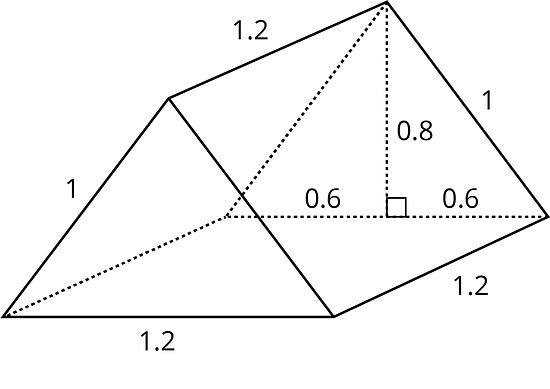
7. Find the surface area of this triangular prism. All measurements are in meters.

• Show Image
  

• Answers

  Area of 2 triangular bases = 2 × ½ × 1.2 m × 0.8 m = 0.96 m²
  Area of the bottom rectangular face = 1.2 m × 1.2 m = 1.44 m²
  Area of two sloping faces = 2 × 1 m × 1.2 m = 2.4 m²
  Surface area = 0.96 m² + 1.44 m² + 2.4 m² = 4.8 m²

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.