Square Roots
More Lessons for Arithmetic
Math Worksheets
In this lesson, we will look at how to find the square roots of perfect squares and the square roots of non-perfect squares.
Square Roots Of Perfect Squares
The opposite of squaring a number is finding the square root.
We know that 4 squared = 42 = 16. The square root of 16 is the number that can be multiplied by itself to get 16, which is 4.
The symbol used for square root is 
. (The symbol is also called the radical sign)
= 4 (The square root of 16 is 4).
Notice that –4 is also a square root of 16.
Check: (–4) × (–4) = 16, i.e. (–4)2 = 16.
We see that the number 16 has two square roots: a positive square root and a negative square root.
For any positive value x, 
We can get the square root of perfect squares in the following way:
Example :
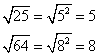
Similarly, for any positive value x, 
Example :
Also, take note that
Example:
Example:
Work out the following:
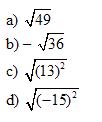
Solution:
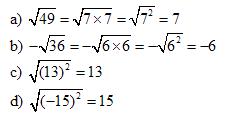
The following video shows how to find the square root of perfect squares.
Square Roots Of Non-Perfect Squares
Square root of numbers that are not perfect squares would be an irrational number. (Irrational numbers are numbers that cannot be written as fractions. and in decimal form, these numbers go on forever and the same pattern of digits is not repeated.)
For example, 
= 1.4142…
Usually, we would need to use a calculator to get the square root of a non-perfect square.
However, if you are curious as to how to calculate the square root without a calculator, have a look at the following video.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.