Solving Multi-Step Equations
Related Pages
Solving Algebraic Equations
More Algebra Lessons
In this lesson, we will learn how to
- Solve multi-step equations with whole numbers
- Solve multi-step equations with fractions
- Solve multi-step equations with decimals
How to solve multi-step equations?
Solving multi-step equations involves using more than one operation to isolate the variable. You’ll combine the techniques you learned for one-step equations and two-step equations along with some additional strategies.
The following diagram shows how to solve multi-step equations. Scroll down the page for more examples and solutions.
Algebra Worksheets
Practice your skills with the following Algebra worksheets:
Printable & Online Algebra Worksheets
To solve a multi-step equation, we could start by trying to simplify the equation by using the distributive property and combining like terms.
- Simplify Each Side of the Equation:
a. Distribute: If there are any parentheses, use the distributive property to multiply the term outside the parentheses by each term inside.
Example: \(3(x + 2) = 3\cdot x + 3\cdot2 = 3x + 6\)
b. Combine Like Terms: If there are like terms on the same side of the equation, combine them by adding or subtracting their coefficients.
Example: \(4y + 7 - 2y = (4y - 2y) + 7 = 2y + 7\)
- Isolate the Variable Term:
a. Move Constant Terms: Use addition or subtraction to move all constant terms to one side of the equation (usually the side opposite the variable term).
Remember to perform the same operation on both sides to keep the equation balanced.
b. Move Variable Terms (if necessary): If there are variable terms on both sides of the equation, use addition or subtraction to move all variable terms to one side (usually the side where the coefficient of the variable will be positive or larger).
Again, perform the same operation on both sides.
-
Isolate the Variable:
Undo Multiplication or Division: If the variable is being multiplied by a coefficient, divide both sides of the equation by that coefficient. If the variable is being divided by a number, multiply both sides by that number. -
Check Your Solution:
a. Substitute: Substitute the value you found for the variable back into the original equation.
b. Verify: Simplify both sides of the equation. If both sides are equal, your solution is correct.
Key Rules
- Reverse PEMDAS: Undo operations in reverse order (Addition/Subtraction before Multiplication/Division).
- Balance the equation: Perform the same operation on both sides.
- Check your solution: Substitute x back into the original equation.
Solving multi-step equations with whole numbers
Consider the equation 2(x + 1) – x = 5. First, we will use the distributive property to remove the parenthesis and then we can combine like terms and then isolate the variable.
Example:
Solve 2(x + 1) – x = 5
Solution:
2(x + 1) – x = 5
2x + 2 – x = 5 (use distributive property)
x + 2 = 5 (combine like terms)
x + 2 – 2 = 5 – 2
x = 3
How to solve multi-step equations by combining like terms and using the distributive property?
Examples:
- 4x + 2x - 3x = 27
- 4a + 1 - a = 19
- 4(y - 1) = 36
- 16 = 2(x - 1) - x
Use distributive property to simplify multi-step equations
Examples:
- 7(w + 20) - w = 5
- 9(x - 2) = 3x + 3
- Lydia inherited a sum of money. She split it into five equal chunks. She invested three parts of the money in a high interest bank account which added 10% to the value. She placed the rest of her inheritance plus $500 in the stock market but lost 20% on that money. If the two accounts end up exactly the same amount of money in them, how much did she inherit?
Solving Multi-Step Equations With Fractions
To solve an equation with fractions, we first try to change it into an equation without fractions. Then, we can solve it using the methods we already know.
Consider the equation 
. To remove the fractions, we would need to multiply each term of the equation with the LCM of the denominator. In this case, we will multiply each term with 4. The 4 will cancel and we are left with equation 2x – 12 = 3. To isolate the variable, we will add 12 to both sides and then divide by 2.
Example:
Solve
Solution:
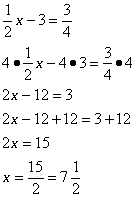
How to solve multi-step equations with fractions?
Examples:
- 1/4 x + 3 = 2
- 1/2 (k - 8) = 6
- 1/2 d + 2 = 3/4
- -3/4 x + 1/4 = 1/2
How to solve Multi-Step Equations with Fractions & Decimals?
Examples:
- 3/2 n - 6 = 22
- 2/5 x + 2 = 3/4
- 0.035m + 9.95 = 12.75
Solving Multi-Step Equations With Decimals
The steps involved in solving multi-step equations with decimals are the same as those in equations with whole numbers. The complication may lie more in the multiplication and division of decimals rather than the steps. Another method would be to multiply each term of the equation by ten (or hundred) to convert the decimals to whole numbers and then solve the equation.
How to solve multi-step equations with decimals?
Examples:
- 0.4x + 9.2 = 10
- 0.4(a + 2) = 2
- 1.2c + 2.6c = 4.56
How to solve multiple step linear equations involving decimals?
- Remove parentheses by using the distributive property. Then combine like terms on each side.
- Add or subtract, as needed, to get all variable terms on one side and all constant terms on the other. Then combine like terms.
- Multiply or divide to solve for the variable.
- Check all possible solutions.
Examples:
Solve each equation.
- 1.2x - 5.12 - 0.9x = 1.6
- 5x - 0.2(x - 4.2) = 1.8
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.