Solve for a Variable in a Formula

In these lessons, we will learn how to solve a formula for a variable. It is also called solving literal equations.

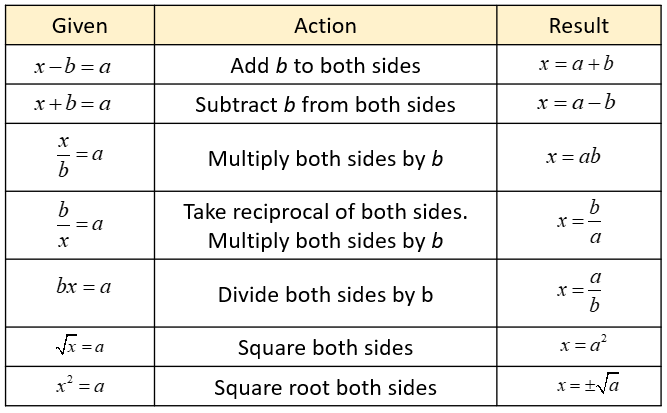
Solving for a variable in a formula involves similar steps to solving for a variable in an equation. Let us review the steps as follows when we need to solve for a variable in a formula.

1. Determine which variable you need to solve or isolate.
   To solve or isolate a variable means to get the variable on one side of the equation by itself.
2. Use inverse operations to move all the other variables or constants to the other side of the equation. In order to keep the equation balanced, the operations need to be applied to both sides of the equation.

 

Printable & Online Algebra Worksheets
Equation Solver Game

Example:

The formula for the area of a circle is A = πr². Solve for r in the formula.

 

Solving a Formula For a Variable This algebra video lesson explains how to solve a formula for a variable.
The formulas include the area of a trapezoid formula, ohm’s law with voltage current and resistance.
The equivalent resistance of two resistors in a parallel circuit.
The geometric mean formula of two numbers.
The time it takes for two people to complete a job working together formula.
The area of a circle formula. The volume of a sphere formula.
The electromotive force of a battery along with internal resistance.

• Show Video Lesson

How to solve a formula with variables for a specified variable?
Examples:

1. Solve for r
   d = rt
2. Solve for h
   A = 1/2 bh
3. Solve for b₂
   A = 1/2(b₁ + b₂)
4. Solve for w
   P = 2L + 2W
5. Write y in terms of x
   y - 3 = 1/3(x - 4)
6. Solve for a
   1/a + 1/b = 1/2

• Show Step-by-step Solutions

Solving formulas for given variables
Examples:

1. c = ipv, solve for v
2. p = a + 3b + 2c, solve for a
   t = 3j + 3v, solve for k

• Show Step-by-step Solutions

Solving an Equation for a Specified Variable
Examples:

1. Solve for Solve for b₁
   A = 1/2h(b₁ + b₂)
2. Solve for z
   3z + x - y = 2x + 4

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.