Find the Slope of a Line
Related Topics:
More Lessons for Grade 8
Math Worksheets
Examples, videos, worksheets, stories and solutions to help Grade 7 students learn how to find the slope of a line given the graph or given two points.
Types of Slopes
There are four main types of slopes: Positive Slope, Negative Slope, Zero Slope, Undefined Slope.
The following diagram shows the types of slope for a line. Scroll down the page for more examples and solutions for the slope of a line.
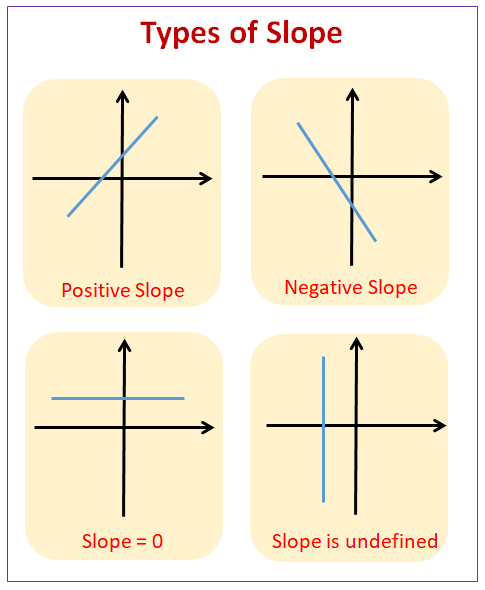
Coordinate Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Coordinate Geometry Worksheets
How to find the slope of a line?
1. Given Two Points on the Line:
If you know two points on the line, say \((x_1, y_1)\) and \((x_2, y_2)\), you can use the slope formula:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
where:
\(m\) represents the slope of the line.
\(y_2 - y_1\) is the “rise” (the vertical change between the two points).
\(x_2 - x_1\) is the “run” (the horizontal change between the two points).
2. Write the Equation of the Line in Slope-Intercept Form:
The slope-intercept form of a linear equation is:
\(y = mx + b\)
where:
\(m\) is the slope of the line.
\(b\) is the y-intercept
If your equation is in this form, the coefficient of \(x\) is the slope.
Types of Slopes
1. Positive Slope:
A line with a positive slope goes upward as you move from left to right on the graph. Think of walking uphill.
The “rise” (vertical change) and the “run” (horizontal change) have the same sign.
Slope Value: \(m > 0\).
2. Negative Slope:
A line with a negative slope goes downward as you move from left to right on the graph. Think of walking downhill.
The “rise” (vertical change) and the “run” (horizontal change) have opposite signs.
Slope Value: \(m < 0\)
3. Zero Slope:
A line with a zero slope is a horizontal line. It doesn’t go up or down. Think of walking on a flat road.
The “rise” (vertical change) is zero for any amount of “run” (horizontal change).
Slope Value: \(m = 0\).
Horizontal lines have equations of the form \(y = b\), where \(b\) is a constant (the y-intercept). The y-value stays the same no matter what the x-value is.
4. Undefined Slope:
A line with an undefined slope is a vertical line. It goes straight up and down. Think of climbing a vertical wall.
Slope Value: Slope is undefined.
When you use the slope formula \(m = \frac{y_2 - y_1}{x_2 - x_1}\), you end up dividing by zero, which is undefined.
Vertical lines have equations of the form \(x = a\), where \(a\) is a constant (the x-intercept). The x-value stays the same no matter what the y-value is.
Finding the Slope of a Line
This covers the concept of slope, what it means and how to find the slope of a line by looking at its graph.
Basic idea of slope, what it means, and how you can determine the slope by looking at a graph.
More examples are included.
Algebraic formula used to find the slope of a line passing through two points.
How to find the slope of a line passing through two points by using the algebraic formula for slope?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.