Sine Ratio Problems

Understanding the Sine Ratio
In a right-angled triangle, the sine of an acute angle is defined as the ratio of the length of the side opposite to that angle to the length of the hypotenuse.

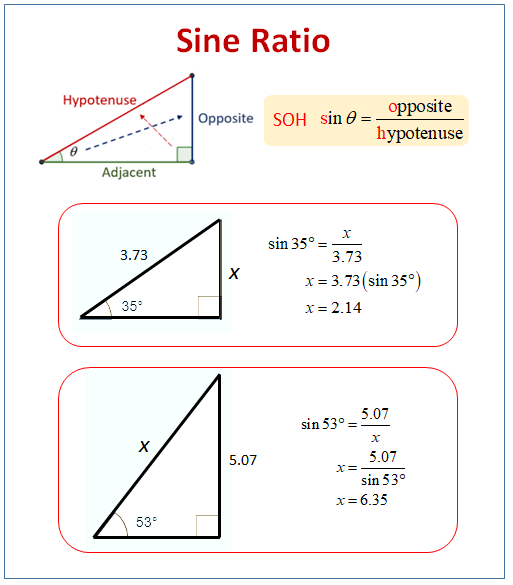
The following diagram shows the sine ratio and examples of using the ratio to find missing side lengths. Scroll down the page for more examples and solutions for the sine ratio.

Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets

When to Use the Sine Ratio
For a given angle θ in a right-angled triangle:
\( sin(θ) = \frac{Opposite}{Hypotenuse} \)
where
Opposite is the side directly across from angle θ.
Hypotenuse is the longest side, opposite the right angle.

Use the sine ratio when:
You know an angle and the opposite side or hypotenuse.
You need to find a missing side or angle in a right-angled triangle.

Steps to Solve Problems Using the Sine Ratio

1. Draw and Label the Right-Angled Triangle
   Read the problem carefully and visualize the situation.
   Draw a right-angled triangle that represents the problem.
   

2. Identify the Knowns and the Unknown
   Determine which angle you are working with (the reference angle).
   Identify the lengths of the sides that are given in the problem.
   Identify the length of the side or the measure of the angle that you need to find.
   

3. Set up the Sine Ratio Equation
   Use the definition of the sine ratio:
   sin(reference angle) = Length of the Opposite Side / Length of the Hypotenuse
   Substitute the known values (the angle and the length of one of the sides) into the equation.
   Let the unknown value be represented by a variable.
   

4. Solve the equation to find the side or the angle.
   Use the sine function if you need to find the side when given the angle.
   Use the inverse sine function (sin⁻¹ or arcsin) on your calculator if you need to find the unknown angle given the sine ratio.

Example:

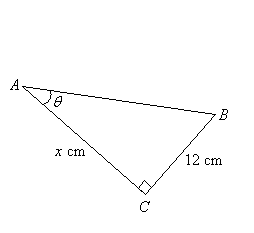
Calculate the length of the side x, given that sin θ = 0.6

Solution:

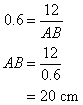
Using Pythagoras’ theorem:

Hints on solving trigonometry problems:

• If no diagram is given, draw one yourself.
• Mark the right angles in the diagram.
• Show the sizes of the other angles and the lengths of any lines that are known
• Mark the angles or sides you have to calculate.
• Consider whether you need to create right triangles by drawing extra lines. For example, divide an isosceles triangle into two congruent right triangles.
• Decide whether you will need Pythagoras theorem, sine, cosine or tangent.
• Check that your answer is reasonable. The hypotenuse is the longest side in a right triangle.

SOH CAH TOA:
A helpful mnemonic to remember the basic trigonometric ratios is SOH CAH TOA:
SOH: Sine = Opposite / Hypotenuse
CAH: Cosine = Adjacent / Hypotenuse
TOA: Tangent = Opposite / Adjacent
For learning about the sine ratio, just focus on the SOH part.

Find Missing Sides

Find the missing length of a triangle using the sine function
These two videos show you how to find the missing length of a triangle using the sine function.
We are given a right triangle and two side lengths and a missing length.
We show a right triangle and label the hypotenuse, and two legs the opposite side and adjacent side according to their relation to θ.

• Show Step-by-step Solutions

• Show Step-by-step Solutions

Trigonometry Basics : SOHCAHTOA
How to find missing sides using sine, cosine and tangent?

• Show Step-by-step Solutions

Find Missing Angles

Trigonometry : using SOHCAHTOA to find missing angles.

• Show Step-by-step Solutions

Trig Ratios - SOH-CAH-TOA
Find missing Angle - Using Inverse Sine, Cosine

• Show Step-by-step Solutions

Sine Function Word Problems

A word problem involving the trigonometric ratio of sine to calculate the height of a pole
Example:
A 55ft wire connects a point on the ground to the top of a pole. The cable makes an angle of 60 degrees to the ground. Find the height of the pole to the nearest foot.

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.