Illustrative Mathematics Grade 8, Unit 2, Lesson 8: Similar Triangles

Related Pages
Illustrative Math
Grade 8

Lesson 8: Similar Triangles

Let’s look at similar triangles.

Illustrative Math Unit 8.2, Lesson 8 (printable worksheets)

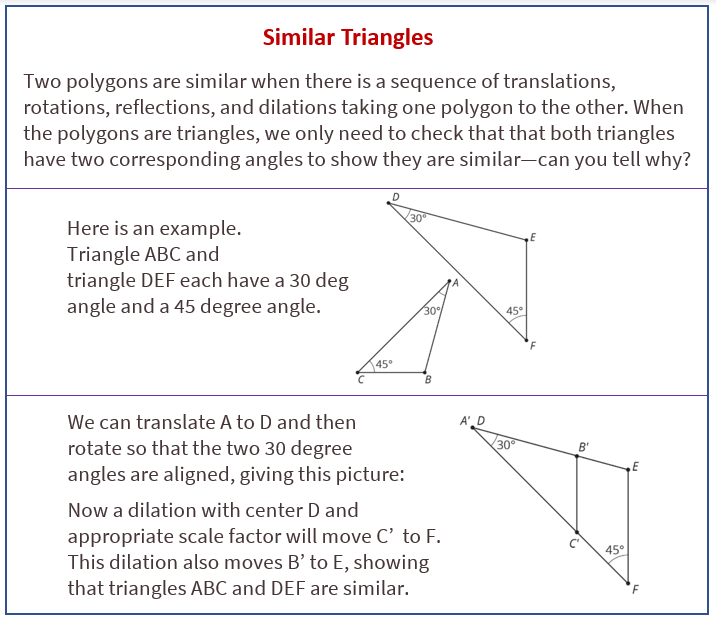
Lesson 8 Summary

The following diagram shows how to decide if two triangles are similar just by looking at their angle measures.

Lesson 8.1 Equivalent Expressions

Create three different expressions that are each equal to 20. Each expression should include only these three numbers: 4, -2, and 10.

• See Video for Whole Lesson

Lesson 8.2 Making Pasta Angles and Triangles

Your teacher will give you some dried pasta and a set of angles.

1. Create a triangle using three pieces of pasta and angle A. Your triangle must include the angle you were given, but you are otherwise free to make any triangle you like. Tape your pasta triangle to a sheet of paper so it won’t move.
   a. After you have created your triangle, measure each side length with a ruler and record the length on the paper next to the side. Then measure the angles to the nearest 5 degrees using a protractor and record these measurements on your paper.
   b. Find two others in the room who have the same angle A and compare your triangles. What is the same? What is different? Are the triangles congruent? Similar?
   c. How did you decide if they were or were not congruent or similar?
2. Now use more pasta and angles A, B, and C to create another triangle. Tape this pasta triangle on a separate sheet of paper.
   a. After you have created your triangle, measure each side length with a ruler and record the length on the paper next to the side. Then measure the angles to the nearest 5 degrees using a protractor and record these measurements on your paper.
   b. Find two others in the room who used your same angles and compare your triangles. What is the same? What is different? Are the triangles congruent? Similar?
   c. How did you decide if they were or were not congruent or similar?
3. Here is triangle PQR. Break a new piece of pasta, different in length than segment PQ.

• Tape the piece of pasta so that it lays on top of line PQ with one end of the pasta at P (if it does not fit on the page, break it further). Label the other end of the piece of pasta S.
• Tape a full piece of pasta, with one end at S, making an angle congruent to ∠PQR.
• Tape a full piece of pasta on top of line PR with one end of the pasta at P. Call the point where the two full pieces of pasta meet T.
  a. Is your new pasta triangle PST similar to △PQR? Explain your reasoning.
  b. If your broken piece of pasta were a different length, would the pasta triangle still be similar to △PQR? Explain your reasoning.

Are you ready for more?

Quadrilaterals ABCD and EFGH have four angles measuring 240°, 40°, 40°, and 40°. Do ABCD and EFGH have to be similar?

• Show Answer

  Yes, ABCD is similar to EFGH.
  Two quadrilaterals that have corresponding congruent angles are similar, if the quadrilaterals do not have parallel sides.

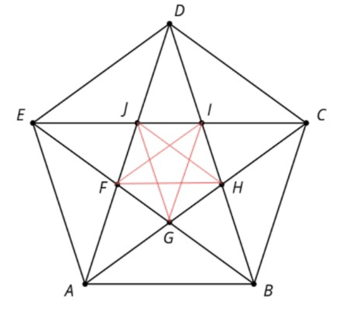
Lesson 8.3 Similar Figures in a Regular Pentagon

1. This diagram has several triangles that are similar to triangle DJI.
   a. Three different scale factors were used to make triangles similar to DJI. In the diagram, find at least one triangle of each size that is similar to DJI.
   b. Explain how you know each of these three triangles is similar to DJI.
2. Find a triangle in the diagram that is not similar to DJI.

Are you ready for more?

Figure out how to draw some more lines in the pentagon diagram to make more triangles similar to DJI.

• Show Answer

  

Lesson 8 Practice Problems

1. In each pair, some of the angles of two triangles in degrees are given. Use the information to decide if the triangles are similar or not. Explain how you know.

• Triangle A: 53, 71, ___; Triangle B: 53, 71, ___
• Triangle C: 90, 37, ___; Triangle D: 90, 53, ___
• Triangle E: 63, 45, ____; Triangle F: 14, 71, ____
• Triangle G: 121, ___, ___; Triangle H: 70, ___, ___

2. a. Draw two equilateral triangles that are not congruent.
   b. Measure the side lengths and angles of your triangles. Are the two triangles similar?
   c. Do you think two equilateral triangles will be similar always, sometimes, or never? Explain your reasoning.
3. In the figure, line BC is parallel to line DE.
   Explain why △ABC is similar to △ADE.
4. The quadrilateral PQRS in the diagram is a parallelogram. Let P’Q’R’S' be the image of PQRS after applying a dilation centered at a point O (not shown) with scale factor 3.
   Which of the following is true?
5. Describe a sequence of transformations for which Quadrilateral P is the image of Quadrilateral Q.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.