Sieve of Eratosthenes
In these lessons, we look into the Sieve of Eratosthenes and its use in finding prime numbers.
Related Pages
Prime Numbers
More Arithmetic Lessons
Free Math Worksheets
A prime number is a whole number that has exactly two factors, 1 and itself.
The Sieve of Eratosthenes is an ancient algorithm that can help us find all prime numbers up to any given limit.
How does the Sieve of Eratosthenes work?
The following example illustrates how the Sieve of Eratosthenes, can be used to find all the
prime numbers that are less than 100.
Step 1: Write the numbers 1 to 100 in ten rows.
Step 2: Cross out 1 because 1 is not a prime.
Step 3: Circle 2 and cross out all multiples of 2. (2, 4, 6, 8, 10, …)
Step 4: Circle 3 and cross out all multiples of 3. (3, 6, 9, 12, 15, …)
Step 5: Circle 5 and cross out all multiples of 5. (5, 10, 15, 20, …)
Step 6: Circle 7 and cross out all multiples of 7. (7, 14, 21, 28, …)
Circle all the numbers that are not crossed out and they are the prime numbers less than 100.
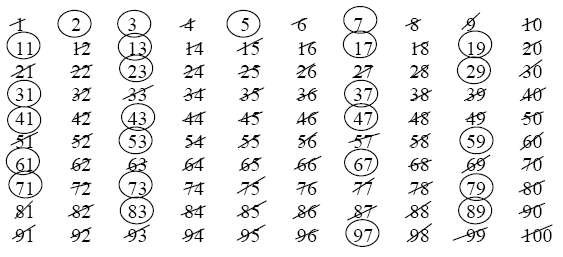
How to use the Sieve of Eratosthenes to find all the prime numbers less than 100?
The Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to
a specified integer. In this case we are using a chart up to 100.
How to find all the prime numbers between 1 and 100 using the technique devised by the ancient Greek mathematician Eratosthenes?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.