Shading Venn Diagrams

What Is A Venn Diagram?

A Venn Diagram is a pictorial representation of the relationships between sets. Shading Venn diagrams is a technique used to visually represent specific regions of interest, such as the intersection, union, complement, or other set operations. By shading certain areas, you can clearly highlight the elements that belong to a particular set or combination of sets.

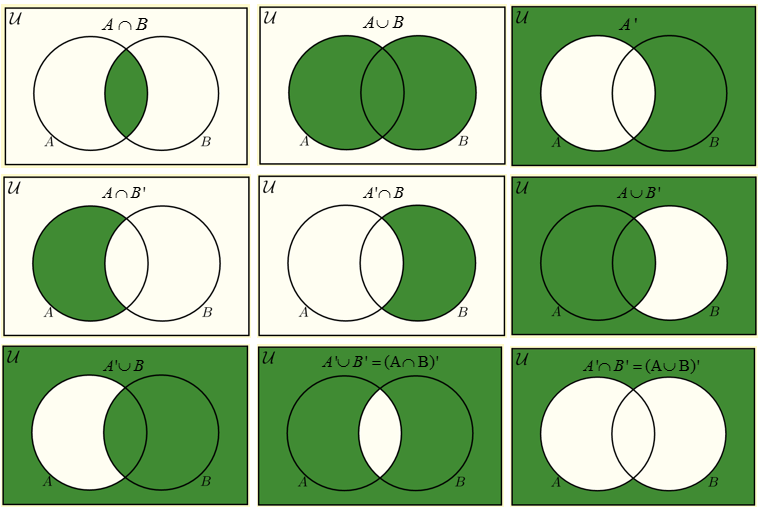
The following figures show how to shade regions of Venn Diagrams for two sets:
A intersect B, A union B, A’, A intersect B’, A’ intersect B, A union B’,
A’ union B, A’ union B’ = (A intersect B)’, A’ intersect B’ = (A union B)’.
Scroll down the page for more examples and solutions on how to shade Venn Diagrams to represent the required regions of two sets and three sets.

 

Venn Diagram Game/Worksheet
Venn Diagrams for: Intersection (A ∩ B), Union (A ∪ B), Complement (A’), Empty Set (∅), Difference (A - B), Symmetric Difference (A Δ B), Outer Region ((A ∪ B)’)

How to shade Venn Diagrams?

• Union (∪): Think “OR” – shade all involved sets.
• Intersect (∩): Think “AND” – shade only overlaps.
• Complement (’): Think “NOT” – shade outside the set.

For more complex expressions, it’s helpful to:

1. Break down the expression into smaller parts.
2. Shade each smaller part on a separate “scratch” diagram.
3. Combine the shaded regions according to the final operation (e.g., union means take all shaded areas, intersection means take only the areas shaded in all intermediate diagrams).

Venn Diagrams: Shading Regions for Two Sets

How to shade the union, intersection and complement of two sets?

1. A ∪ B'
2. A’ ∩ B'
3. (A ∪ B)'

• Show Video Lesson

Basic Venn Diagram Shading

This video lesson covers the following cases:

1. A ∪ B
2. A ∩ B
3. A’ ∪ B
4. A ∩ B'
5. A ∪ B ∪ C
6. A ∩ B ∩ C

• Show Video Lesson

Shading Venn Diagrams

The video lesson covers the following situations:

1. A ∩ B
2. (A ∩ B)'
3. A ∪ B'
4. A ∩ B'
5. B'
6. (A ∪ B)'
7. A ∩ B = { }
8. A ∩ C
9. (A ∩ C) ∪ B
10. (A ∩ C) ∩ B'

• Show Video Lesson

Venn Diagrams: Shading Regions With Three Sets

How To Shade Regions Of Venn Diagrams Involving Three Sets? Part 1 of 2

1. (A ∩ B) ∩ C
2. (A ∪ B) ∩ C

• Show Video Lesson

How To Shade Regions Of Venn Diagrams Involving Three Sets? Part 2 of 2

3. (A ∪ B)’ ∩ C
4. (A’ ∩ B’) ∩ C'

• Show Video Lesson

Venn Diagram Shading Calculator Or Solver

Enter an expression like (A Union B) Intersect (Complement C) to describe a combination of two or three sets and get the notation and Venn diagram. Use parentheses, Union, Intersection, and Complement.

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.