Illustrative Mathematics Grade 8, Unit 6, Lesson 5: Describing Trends in Scatter Plots

Related Pages
Illustrative Math
Grade 8

Lesson 5: Fitting a Line to Data

Let’s look for associations between variables.

Illustrative Math Unit 8.6, Lesson 5 (printable worksheets)

Lesson 5 Summary

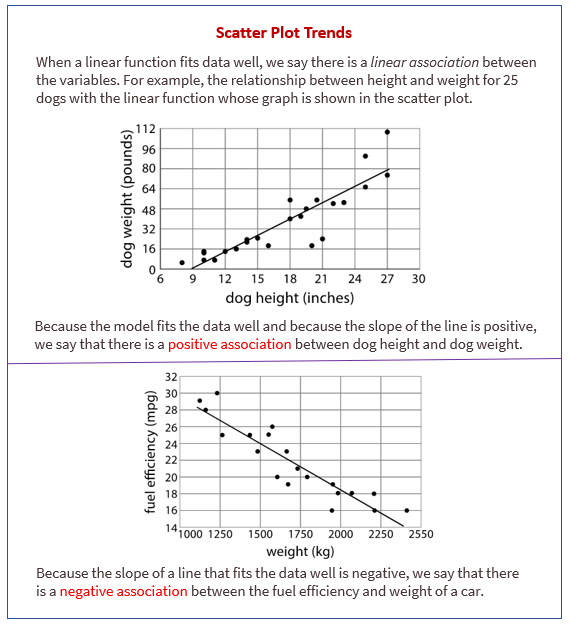
The following diagram shows how to say whether data in a scatter plot has a positive or negative association (or neither).

Lesson 5.1 Which One Doesn’t Belong: Scatter Plots

Which one doesn’t belong?

• See Video for Whole Lesson

Lesson 5.2 Shine Bright

Experiment with finding lines to fit the data. Drag the points to move the line. You can close the expressions list by clicking on the double arrow.
Here is a scatter plot. Experiment with different lines to fit the data. Pick the line that you think best fits the data. Compare it with a partner’s..
Open Applet
2. Here is a different scatter plot. Experiment with drawing lines to fit the data. Pick the line that you think best fits the data. Compare it with a partner’s.
Open Applet
3. In your own words, describe what makes a line fit a data set well.

Lesson 5.3 Good Fit Bad Fit

The scatter plots both show the year and price for the same 17 used cars. However, each scatter plot shows a different model for the relationship between year and price.

1. Look at Diagram A.
   a. For how many cars does the model in Diagram A make a good prediction of its price?
   b. For how many cars does the model underestimate the price?
   c. For how many cars does it overestimate the price?
2. Look at Diagram B.
   a. For how many cars does the model in Diagram B make a good prediction of its price?
   b. For how many cars does the model underestimate the price?
   c. For how many cars does it overestimate the price?
   
3. For how many cars does the prediction made by the model in Diagram A differ by more than $3,000? What about the model in Diagram B?
4. Which model does a better job of predicting the price of a used car from its year?

Lesson 5.4 Practice Fitting Lines

1. Is this line a good fit for the data? Explain your reasoning.
2. Draw a line that fits the data better.
3. Is this line a good fit for the data? Explain your reasoning.
4. Draw a line that fits the data better.

Are you ready for more?

These scatter plots were created by multiplying the x-coordinate by 3 then adding a random number between two values to get the y-coordinate. The first scatter plot added a random number between -0.5 and 0.5 to the y-coordinate. The second scatter plot added a random number between -2 and 2 to the y-coordinate. The third scatter plot added a random number between -10 and 10 to the y-coordinate.

1. For each scatter plot, draw a line that fits the data.
2. Explain why some were easier to do than others.

Lesson 5 Practice Problems

1. a. Draw a line that you think is a good fit for this data. For this data, the inputs are the horizontal values, and the outputs are the vertical values.
   b. Use your line of fit to estimate what you would expect the output value to be when the input is 10.
2. Here is a scatter plot that shows the most popular videos in a 10-year span.
   a. Use the scatter plot to estimate the number of views for the most popular video in this 10-year span.
   b. Estimate when the 4th most popular video was released.
3. A recipe for bread calls for 1 teaspoon of yeast for every 2 cups of flour.
   a. Name two quantities in this situation that are in a functional relationship.
   b. Write an equation that represents the function.
   c. Draw the graph of the function. Label at least two points with input-output pairs.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.