Illustrative Mathematics Grade 7, Unit 1, Lesson 8: Scale Drawings and Maps

Related Pages
Illustrative Math
Grade 7

Lesson 8: Scale Drawings and Maps

Let’s use scale drawings to solve problems.

Illustrative Math Unit 7.1, Lesson 8 (printable worksheets)

Lesson 8 Summary

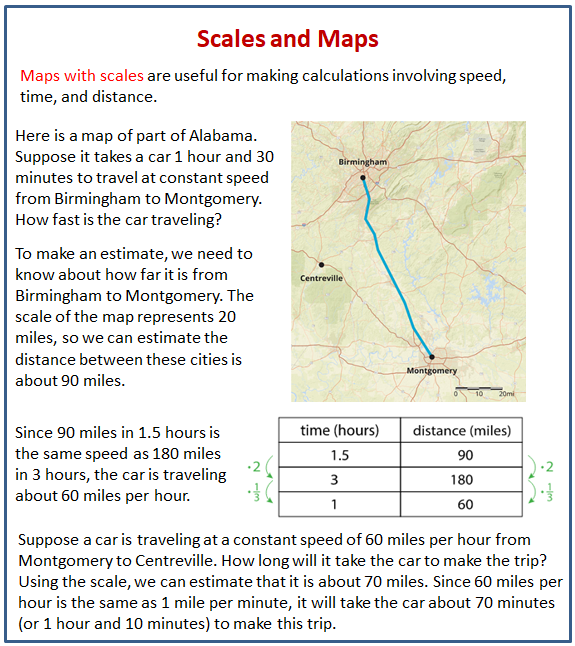
The following diagram shows how to use a map and its scale to solve problems about traveling.

Lesson 8.1 A Train and a Car

Two cities are 243 miles apart.

• It takes a train 4 hours to travel between the two cities at a constant speed.
• A car travels between the two cities at a constant speed of 65 miles per hour.
  Which is traveling faster, the car or the train? Be prepared to explain your reasoning.
  

• See Video for Whole Lesson

Lesson 8.2 Driving on I-90

1. A driver is traveling at a constant speed on Interstate 90 outside of Chicago. If she traveled from Point A to Point B in 8 minutes, did she obey the speed limit of 55 miles per hour? Explain your reasoning.
2. A traffic helicopter flew directly from Point A to Point B in 8 minutes. Did the helicopter travel faster or slower than the driver? Explain or show your reasoning.
   Use the Distance tool to measure the shortest distance between two points.
   Open Applet

Lesson 8.3 Biking through Kansas

A cyclist rides at a constant speed of 15 miles per hour. At this speed, about how long would it take the cyclist to ride from Garden City to Dodge City, Kansas?

Are you ready for more?

Jada finds a map that says, “Note: This map is not to scale.” What do you think this means? Why is this information important?

• Show Answer

  Not to scale means we cannot use the distances on the map to find the actual distances between locations.
  
  

Lesson 8 Practice Problems

1. Here is a map that shows parts of Texas and Oklahoma.
   a. About how far is it from Amarillo to Oklahoma City? Explain your reasoning.
   b. Driving at a constant speed of 70 miles per hour, will it be possible to make this trip in 3 hours? Explain how you know.
   
2. A local park is in the shape of a square. A map of the local park is made with the scale 1 inch to 200 feet.
   a. If the park is shown as a square on the map, each side of which is one foot long, how long is each side of the square park?
   b. If a straight path in the park is 900 feet long, how long would the path be when represented on the map?
   

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.